Variante: Aus einer Zeichnung ablesen
Was im Steigungsdreieck nach oben (oder nach unten) gegangen wird, steht im Zähler. In diesem Fall musste man ja 2 cm nach oben gehen, daher steht im Zähler von m die Zahl 2.
Die Steigung m der Geraden g1 lautet deshalb: m = +![]()
Nun können wir die Gleichung von angeben: ![]()
Nach demselben Prinzip verfahren wir nun auch bei den drei anderen Geraden:
In Abb. 8.46b ist die Gerade dargestellt. Der Schnittpunkt mit der y-Achse hat die Koordinaten T(0; 2). Deshalb gilt:t=2
In Abb. 8.47b kannst du die Gerade mit ihrem Steigungsdreieck sehen. Um von T(0; 2) zum Punkt P(1; -1) zu gelangen, musste man 1 cm nach rechts und 3 cm nach unten gehen. Da hier nach unten gegangen wurde, ist die Steigung m negativ.
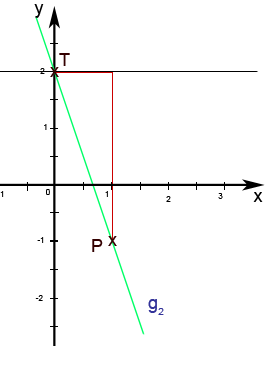
Abb. 8.47b
Was im Steigungsdreieck nach rechts gegangen wird, steht im Nenner. In diesem Fall musste man ja 1 cm nach rechts gehen, daher steht im Nenner von m die Zahl 1.
Was im Steigungsdreieck nach unten (bzw. nach oben) gegangen wird, steht im Zähler. In diesem Fall musste man ja 3 cm nach unten gehen, daher steht im Zähler von m die Zahl 3.
Die Steigung m der Geraden lautet deshalb: m = ![]()
Nun können wir die von g2 angeben: ![]()
In Abb.

