Variante: Aus einer Zeichnung ablesen
Gut abzulesen ist der Schnittpunkt mit der y-Achse T(0; -1). Daher weiß man sofort, dass der y-Achsenabschnitt t = -1 ist.
Nun muss m ermittelt werden. Dazu zeichnen wir das Steigungsdreieck ein. Betrachte dazu Abb. 8.47a! Zusätzlich zu dem y-Achsenschnittpunkt T(0; -1) ist auch der Punkt P(3; 1) eindeutig abzulesen. Zwischen diesen beiden Punkten ist das Steigungsdreieck gezeichnet. Da P rechts von T liegt, ist man vom Schnittpunkt mit der y-Achse T waagrecht nach rechts und dann nach oben zum Punkt P gegangen.
Hinweis: Versuche das Steigungsdreieck immer so zu zeichnen, dass du nach rechts (und nicht nach links) vom einen zum anderen Punkt gehst! Nur dann gilt nämlich, dass die Steigung m positiv ist, wenn man danach nach oben geht, bzw. dass m negativ ist, wenn man danach nach unten geht. Würdest du nach links gehen, wäre es genau umgekehrt!
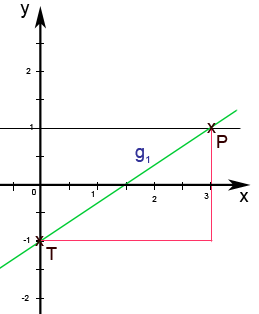
Abb. 8.47a
Wie man in dieser Zeichnung erkennen kann, muss man 3 cm nach rechts und 2 cm nach oben gehen, um von T zum Punkt P zu kommen. Da man nach oben (und nicht nach unten) gehen musste, ist die Steigung m positiv.Wir denken uns m als Bruch.
Was im Steigungsdreieck nach rechts gegangen wird, steht im Nenner. In diesem Fall musste man ja 3 cm nach rechts gehen, daher steht im Nenner von m die Zahl 3.

