Variante: Aus einer Zeichnung ablesen
8.48c ist die Gerade h3 dargestellt. Der Schnittpunkt mit der y-Achse ist nicht eindeutig ablesbar. Daher wird zuerst das Steigungsdreieck eingezeichnet. Gut ablesbar sind die beiden Punkte P1(-3;-1) und P2(2;3) . Um das Steigungsdreieck zu zeichnen, gehen wir von P1 ausgehend um 5 cm waagrecht nach rechts und dann 4 cm nach oben. In Abb. 8.49c ist die Gerade h3 mit ihrem Steigungsdreieck zu sehen.
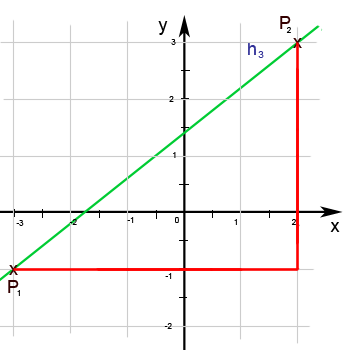
Abb. 8.49c
Die Steigung m lautet daher: m = +![]()
Nun setzen wir diesen Wert für m und die Koordinaten des Punktes für x und y in die allgemeine Geradengleichung y = mx+t ein. Da positive Koordinaten hat, aber nicht, verwenden wir besser zum Einsetzen in die allgemeine Geradengleichung. Verwende also im
mer den Geradenpunkt mit den einfacheren Koordinaten!
![]()
![]() ∣
∣ ![]()
![]()
t =1,4
Nachdem wir jetzt m und t ermittelt haben, können wir nun die Geradengleichung von h3 angeben:
![]()
In Abb. 8.48d ist die Gerade h4 dargestellt.

