Variante: Aus einer Zeichnung ablesen
In Abb. 8.48b ist die Gerade h2 dargestellt. Der Schnittpunkt mit der y-Achse ist nicht eindeutig ablesbar. Daher wird zuerst das Steigungsdreieck eingezeichnet. Gut ablesbar sind die beiden Punkte P1 (-2;4) und P2 (2;0,5). Um das Steigungsdreieck zu zeichnen, gehen wir von P1 ausgehend um 4 cm waagrecht nach rechts und dann 3,5 cm nach unten. Um zu vermeiden, dass bei m im Zähler eine Dezimalzahl steht, zählen wir besser mit Kästchen. Wir gehen also 8 Kästchen nach rechts und 7 Kästchen nach unten. Die Verwendung von Kästchen statt cm bei der Ermittlung von m entspricht eigentlich nur einem Erweitern des Bruchs mit der Zahl 2. In Abb. 8.49b ist die Gerade h2 mit ihrem Steigungsdreieck zu sehen.
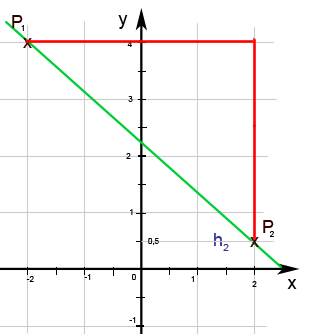
Abb. 8.49b
Die Steigung m lautet daher: m =![]()
Nun setzen wir diesen Wert für m und die Koordinaten des Punktes P1 (-2;4) für x und y in die allgemeine Geradengleichung y = mx+t ein:
![]()
![]() ∣
∣![]()
![]()
t = 2,25
Nachdem wir jetzt m und t ermittelt haben, können wir nun die Geradengleichung von h2 angeben:
![]()
In Abb.

