c) Zwei verschiedene Geradenpunkte P1 und P2 gegeben
(Nun ist m berechnet;der y-Achsenabschnitt t muss noch berechnet werden.)
· Setzte dazu den gerade berechneten Wert für m und die Koordinaten eines der beiden Punkte 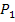 oder
oder 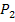 für x und y in die allgemeine Geradengleichung
für x und y in die allgemeine Geradengleichung![]() y = mx+t ein!
y = mx+t ein!
Anmerkung:Es ist völlig egal, welchen Geradenpunkt du verwendest. Nimm einfach denjenigen mit den einfacheren Koordinaten! Du darfst aber nicht die x-Koordinate des einen und die y-Koordinate des anderen Punkts verwenden;das wäre falsch!
· Löse die entstandene Gleichung nach t auf!
· Setze m und t in die allgemeine Geradengleichung y = mx+t ein!
Hinweis:Es gibt noch eine andere Methode, wie die Geradengleichung ermittelt werden kann, wenn die Steigung m und ein weiterer Geradenpunkt P bekannt sind. Manche Realschullehrer verlangen, dass nach der Berechnung von m in die sogenannte Punktsteigungsform der Gerade eingesetzt wird. Vergleiche dazu a) Geradengleichung ermitteln mit m und einem Punkt P:2.Methode mit Punkt-Steigungsform!
Bsp.: Berechne die Gleichung der Geraden g, die durch die Punkte P(-2;-2,5) und Q(2;3) verläuft!
Gegeben: P(-2;-2,5) Q(2;3)
Allgemeine Geradengleichung:y = mx+t
Vektor 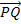 bilden:
bilden: 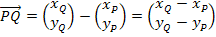
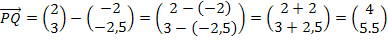
Vertauschen von oberer und unterer Koordinate;als Bruch schreiben: m = 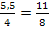
Nun haben wir m berechnet. Um t zu berechnen, gehen wir vor wie bereits in der ersten Methode gezeigt:
Wir setzen m und einen der beiden Geradenpunkte in die allgemeine Geradengleichung y = mx+t ein. In diesem Fall nehmen wir am besten Q(2;3) wegen der einfacheren Koordinaten:

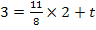
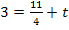
![]() ∣
∣ 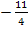
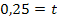
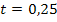
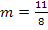 und
und 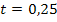 einsetzen in g:
einsetzen in g: 
![]()
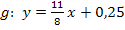
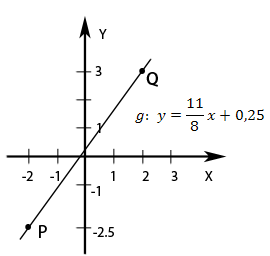
Hinweis:Es gibt noch eine andere Methode, wie die Geradengleichung ermittelt werden kann, wenn die Steigung m und ein weiterer Geradenpunkt P bekannt sind. Manche Realschullehrer verlangen, dass nach der Berechnung von m in die sogenannte Punktsteigungsform der Gerade eingesetzt wird. Vergleiche dazu a) Geradengleichung ermitteln mit m und einem Punkt P:2.Methode mit Punkt-Steigungsform!
|
Zusammenfassung:
Geradengleichung berechnen mit zwei Geradenpunkte · Berechnung von m mit Hilfe der zwei Geradenpunkte 1. Methode: 2. Methode: · Berechnung von t mit Hilfe von m und einem Geradenpunkt (Verwende für die weitere Rechnung den einfacheren der beiden gegebenen Geradenpunkte!) 1. Methode: Ohne Verwendung der „Punkt-Steigungsform“ · Setze m und für x und y die Koordinaten des Geradenpunkts in die allgemeine Geradengleichung y = mx+t ein! · Löse nach t auf! · Setze m und t in die allgemeine Geradengleichung y = mx+t ein! 2. Methode: Mit der „Punkt-Steigungsform“ einer Geraden
· Punkt-Steigungsform · Setze die Steigung m und für · Vereinfache den Funktionsterm, indem du m in die Klammer hineinmultiplizierst und dann zusammenfasst! |
- Page 2 of 2
- « Previous
- 1
- 2
- Next »

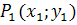 und
und 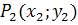 :
: 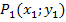 und
und 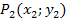
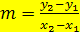

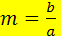
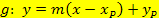
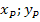 )
)  g
g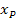 und
und  den Geradenpunkt P(
den Geradenpunkt P( 