c) Zwei verschiedene Geradenpunkte P1 und P2 gegeben

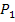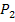Gegeben sind die beiden Punkte und . Gesucht ist die Gerade g, die durch diese beiden Punkte verläuft.

Zuerst muss die Steigung m mit Hilfe der zwei Geradenpunkte berechnet werden.

Dafür gibt es zwei verschiedene Rechenwege. Die zuerst erklärte Methode wird am häufigsten angewendet;in Realschulen wird allerdings auch die als zweites gezeigte Methode verwendet.

Schau einfach in deinem Mathe-Schulheft nach, welche Methode dein Lehrer in der Schule benutzt hat! Nur diese Methode zur Berechnung von m mit Hilfe zweier Geradenpunkte musst du können.

Berechnung von m mit Hilfe der zwei Geradenpunkte 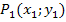und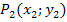

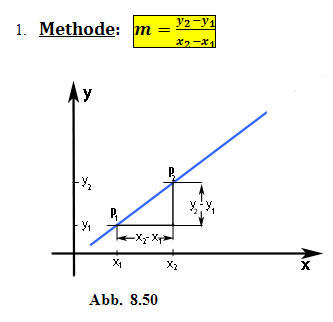
Anleitung:

·        Setzte die Koordinaten der Punkte 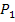und 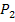in die Formel 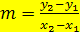ein!

Anmerkung:Es ergibt sich übrigens dasselbe Ergebnis, wenn man mit der Formel 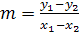rechnet. Durch das Umdrehen der Reihenfolge im Zähler und Nenner drehen sich sowohl im Zähler als auch im Nenner nur die Vorzeichen um. Da sich beideund Nenner, umdrehen, bleibt das Vorzeichen der Steigung m insgesamt unverändert. Es ergibt sich dasselbe Ergebnis für m. Vorzeichen, also im Zähler

Wenn du beispielsweise die beiden Geradenpunkte A und B hast, ist es daher egal, welchen Punkt du als ersten Punkt 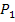und welchen du als zweiten Punkt 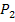ansiehst. Du musst dich nur festlegen. Rechnest du im Zähler 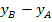, musst du im Nenner auch 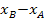rechnen, und nicht andersherum! Damit du nicht durcheinander kommst, solltest du dir allerdings eine feste Methode angewöhnen:Z. B.:„Immer den hinteren minus den vorderen Punkt!“

(Nun ist m berechnet;der y-Achsenabschnitt t muss noch berechnet werden.)

·        Setzte dazu den gerade berechneten Wert für m und die Koordinaten eines der beiden Punkte 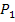oder 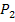für x und y in die allgemeine Geradengleichung y = mx+t ein!

Anmerkung:Es ist völlig egal, welchen Geradenpunkt du verwendest. Nimm einfach denjenigen mit den einfacheren Koordinaten! Du darfst aber nicht die x-Koordinate des einen und die y-Koordinate des anderen Punkts verwenden;das wäre falsch!

·        Löse die entstandene Gleichung nach t auf!

·        Setze m und t in die allgemeine Geradengleichung y = mx+t ein!

Bsp.:  Berechne die Gleichung der Geraden g, die durch die Punkte      P(-2;-2,5) und Q(2;3) verläuft!

Gegeben:    P(-2;-2,5)     Q(2;3)

Allgemeine Geradengleichung:y = mx+t

m berechnen mit der Formel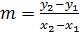

Wir sehen den Punkt P(-2;-2,5) als 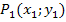und den Punkt Q(2;3) als 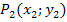an. (Man hätte es auch umgekehrt machen können;man muss sich aber einmal festlegen, bevor man in die Steigungsformel einsetzt.) Die Koordinaten der Punkte werden in die Formel eingesetzt:

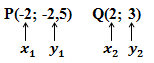
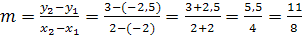Achte besonders auf die Vorzeichen!

Um t zu berechnen, setzen wir nun m und einen der beiden Geradenpunkte in die allgemeine Geradengleichung y = mx+t ein. In diesem Fall nehmen wir am besten Q(2;3) wegen der einfacheren Koordinaten:

∣

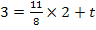
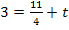
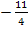
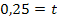
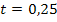
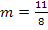und 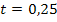einsetzen in  g:

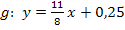
Anmerkung:

Falls du im Unterricht die Punkt-Steigungsform 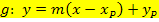gelernt hast, kannst du natürlich die bereits ausgerechnete Steigung m und einen der Geradenpunkte darin einsetzen. Vergleiche dazu das Kapitel Geradengleichung rechnerisch ermitteln:Steigung m und ein Geradenpunkt P gegeben:       2.Methode mit Punkt-Steigungsform!

2.     Methode: Steigung m mit Hilfe des Vektors 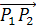ermitteln       (Nur für Realschule)

·        Bilde zuerst den Vektor !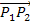

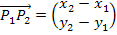Erinnere dich an die Regel „Spitze minus Fuß“!

Um aus dem Vektor 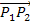die Steigung m zu bilden, vertauscht du die obere mit der unteren Zeile, lässt die Vektorklammern weg und ziehst stattdessen einen Bruchstrich!

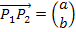
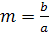
Du hättest auch den Vektor 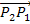verwenden dürfen;das Ergebnis für m wäre trotzdem dasselbe.

---