Wie berechnet man sin(arctanx),sin(arccosx), cos(arcsinx) und cos(arctanx)?

Es gelten die folgenden Zusammenhänge:

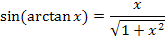
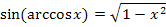
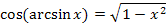
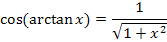
Nur für sehr interessierte Schüler einer mathematisch/technischen FOS bzw. BOS, die vielleicht im Anschluss ein Ingenieursstudium planen:

Wie kommt man auf die oben genannten Zusammenhänge? Das erschließt sich erst nach genauerer Überlegung am Einheitskreis. Um die Herleitungen nachzuvollziehen zu können, musst du die Definitionen der trigonometrischen Funktionen klar vor Augen haben.

Wiederholung der Definitionen von Sinus, Kosinus und Tangens am Einheitskreis:

Der Sinus 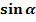ordnet jedem Winkel 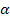(im Bogen- oder Gradmaß) die jeweilige y-Koordinate des zugehörigen Punktes auf dem Einheitskreis zu.

Der Kosinus 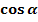ordnet jedem Winkel 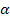(im Bogen- oder Gradmaß) die jeweilige x-Koordinate des zugehörigen Punktes auf dem Einheitskreis zu.

Der Tangens 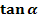ordnet jedem Winkel 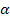(im Bogen- oder Gradmaß) die Länge des jeweiligen Tangentenabschnitts am Einheitskreis zu.

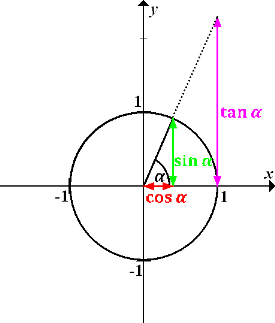
Abb.:Sinus, Kosinus und Tangens am Einheitskreis

Im rechtwinkligen Dreieck gilt:

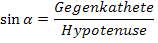
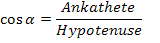
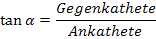
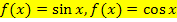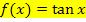Wenn man sich mit den Funktionen und beschäftigt, steht x grundsätzlich für den Winkel im Bogenmaß. (Taschenrechnereinstellung:RAD)

Bei der Sinus-Funktion 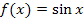stellt der Funktionswert 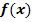laut Definition die y-Koordinate des Punktes auf dem Einheitskreis zum Winkel x dar.

Bei der Kosinus-Funktion 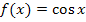stellt der Funktionswert 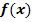laut Definition die x-Koordinate des Punktes auf dem Einheitskreis zum Winkel x (im Bogenmaß) dar.

Bei der Tangens-Funktion 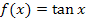stellt der Funktionswert 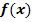laut Definition die Länge des Tangentenabschnitts bezüglich des Einheitskreises zum Winkel x (im Bogenmaß) dar.

Ziemlich verwirrend, dass x hier für einen Winkel (im Bogenmaß) steht und bei der Kosinus-Funktion der Funktionswert 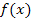, also die y-Koordinate des Punktes auf der Kosinus-Funktion, der x-Koordinate des Punktes auf dem Einheitskreis entspricht. (Sorry, aber einfacher lässt sich das nicht erklären. Das ist leider so festgelegt.)

Bei der Sinus-Funktion ist es etwas einleuchtender:Dem Winkel x im Bogenmaßordnet die Sinusfunktion die zugehörige y-Koordinate des Punktes auf dem Einheitskreis zu. Der Funktionswert 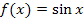, also die y-Koordinate eines Punktes auf der Sinus-Funktion, entspricht somit der y-Koordinate des Punktes auf dem Einheitskreis, der zum Winkel x gehört.

Nun zu den jeweiligen Umkehrfunktionen von Sinus-, Kosinus und Tangens-Funktion. Wenn man die Definitionsmenge entsprechend einschränkt, lassen sich die trigonometrischen Funktionen umkehren. (Darauf wollen wir hier nicht näher eingehen.)

Die Umkehrfunktion zu 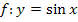ist die Arkussinus-Funktion .

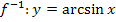Die Umkehrfunktion zu 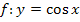ist die Arkuskosinus-Funktion .

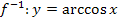Die Umkehrfunktion zu 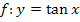ist die Arkustangens-Funktion .

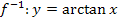Du weißt, dass bei einer Umkehrfunktion im Vergleich zur Funktion selbst x und y vertauscht sind. Die Zuordnung erfolgt also umgekehrt wie bei der zugehörigen Funktion.

Wie kann man nun aber den folgenden Ausdruck herleiten?

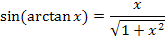
Die Tangensfunktion ordnet dem Winkel x den zugehörigen Tangentenabschnitt am Einheitskreis zu;die Arkustangensfunktion ordnet umgekehrt dem Tangentenabschnitt am Einheitskreis den entsprechenden Winkel (im Bogenmaß) zu.

Der Funktionswert 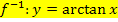entspricht somit einem Winkel am Einheitskreis.

Das Argument x der Arkustangensfunktion entspricht dem Tangentenabschnitt am Einheitskreis.

Übersicht:

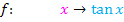
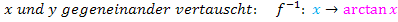
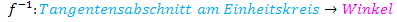
Bei dem Winkel handelt es sich logischerweise wieder um einen Winkel im Bogenmaß. In den folgenden Abbildungen (Abb. 1 bis 4) ist der jeweilige Winkel allerdings nicht als Bogen am Einheitskreis eingezeichnet, sondern zur einfacheren Darstellung als „normaler Winkel“. Betrachte nun die folgende Abbildung!

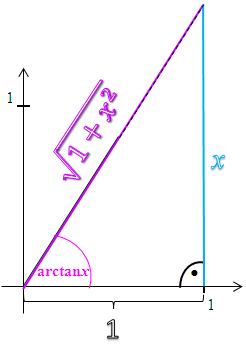
Abb. 1 Zur Herleitung der Formel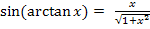

Hinweis zur Abbildung:Strenggenommen ist arctanx der Bogen auf dem Einheitskreis und nicht der Winkel im Gradmaß.

Man kann sich den Zusammenhang 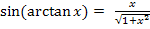jedoch besser erschließen, wenn man sich arctanx als „normalen Winkel“ vorstellt.

Wie kommt man jetzt auf 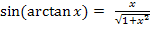? Wie oben schon erwähnt gilt:

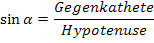
Dem Winkel 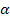entspricht in diesem Fall arctanx. Die Gegenkathete ist hier x. Die Hypotenuse liegt bekanntlich gegenüber des rechten Winkels. Die Hypotenuse, d.h. die Länge des schrägen lila Strichs, ist noch unbekannt.

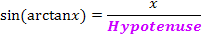
Damit leuchtet es ein, dass 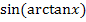dem Ausdruck x / Hypotenuse entspricht. Wir berechnen die Länge der Hypotenuse mit Hilfe des Satzes von Pythagoras. Die eine Kathete ist 1;die andere Kathete ist x.

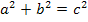
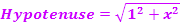
Somit gilt: .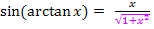

Nun ist dir hoffentlich klar, wie man auf diesen Zusammenhang gekommen ist.

Entsprechend leiten wir als nächstes die Formel 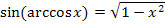her.

Da die Kosinus-Funktion dem Winkel x die zugehörige x-Koordinate des Punktes auf dem Einheitskreis zuordnet, ordnet die Arkuskosinus-Funktion umgekehrt der x-Koordinate des Punktes auf dem Einheitskreis den entsprechenden Winkel (im Bogenmaß) zu.

Der Funktionswert 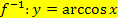entspricht somit einem Winkel am Einheitskreis.

Das Argument x der Arkuskosinus-Funktion entspricht der x-Koordinate des Punktes auf dem Einheitskreis.

Übersicht:

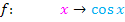
Der Winkel ist eigentlich im Bogenmaß;daher auch die Bezeichnung „Arkus“ lat. Bogen. In der folgenden Abbildung ist der Winkel allerdings nicht als Bogen am Einheitskreis eingezeichnet, sondern als „normaler Winkel“. Betrachte nun die folgende Abbildung!

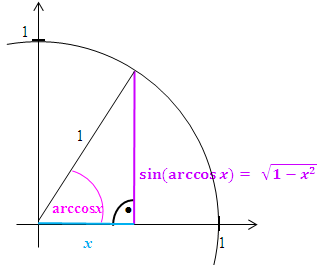
Abb. 2 Zur Herleitung der Formel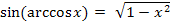

Hinweis zur Abbildung:Strenggenommen ist arccosx der Bogen auf dem Einheitskreis und nicht der Winkel im Gradmaß.

Doch kannst du dir den Zusammenhang 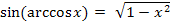sicher besser erschließen, wenn du dir arccosx als normalen Winkel vorstellst.

Wie kommt man jetzt auf 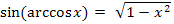? Wie oben schon erwähnt gilt:

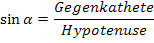
Dem Winkel 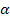entspricht in unserem Fall arccosx. Die Hypotenuse liegt gegenüber des rechten Winkels;sie hat hier die Länge 1, also den Radius des Einheitskreises. Die Gegenkathete (die Länge des senkrechten lila Strichs) ist gesucht.

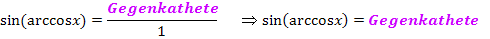
Damit leuchtet es ein, dass 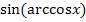der Länge der Gegenkathete (bezüglich des Winkels arccosx) entspricht. Wir berechnen die Gegenkathete mit Hilfe des Satzes von Pythagoras. Die Hypotenuse ist 1;die andere Kathete, also die Ankathete (bezüglich des Winkels arccosx) ist x.

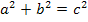
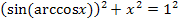
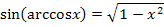
Nun ist dir hoffentlich klar, warum dieser Zusammenhang gilt.

Weiter mit der Herleitung der nächsten Formel: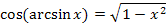

Da die Sinusfunktion dem Winkel x die zugehörige y-Koordinate des Punktes auf dem Einheitskreis zuordnet, ordnet die Arkussinusfunktion umgekehrt der y-Koordinate des Punktes auf dem Einheitskreis den entsprechenden Winkel (im Bogenmaß) zu.

Der Funktionswert 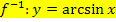entspricht somit einem Winkel am Einheitskreis.

Das Argument x der Arkussinusfunktion entspricht der y-Koordinate des Punktes auf dem Einheitskreis.

Übersicht:

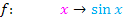
Der Winkel ist natürlich wieder ein Winkel im Bogenmaß. In der folgenden Abbildung ist der Winkel allerdings nicht als Bogen am Einheitskreis eingezeichnet, sondern als „normaler Winkel“. Betrachte nun die folgende Abbildung!

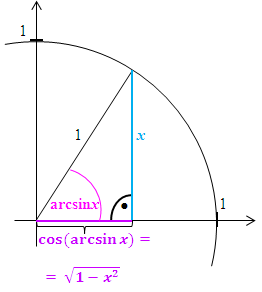
Abb. 3 Zur Herleitung der Formel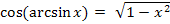

Hinweis zur Abbildung:Strenggenommen ist arcsinx der Bogen auf dem Einheitskreis und nicht der Winkel im Gradmaß.

Doch kannst du dir den Zusammenhang 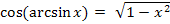sicher besser erschließen, wenn du dir arcsinx als normalen Winkel vorstellst.

Wie kommt man jetzt auf 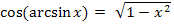? Wie oben schon erwähnt gilt:

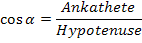
Dem Winkel 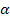entspricht in unserem Fall arcsinx. Die Hypotenuse liegt gegenüber des rechten Winkels;sie hat hier die Länge 1, also den Radius des Einheitskreises. Die Ankathete (die Länge des waagrechten lila Strichs) ist gesucht.

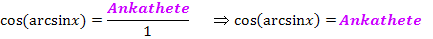
Damitist klar, dass 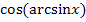der Länge der Ankathete (bezüglich des Winkels arcsinx) entspricht. Wir berechnen sie mit Hilfe des Satzes von Pythagoras. Die Hypotenuse ist 1;die andere Kathete, also die Gegenkathete (bezüglich des Winkels arcsinx) ist x.

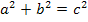
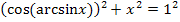
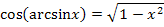
Nun ist dir hoffentlich klar, warum dieser Zusammenhang gilt.

Entsprechend gehen wir auch bei der Herleitung der Formel 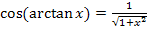vor.

Da die Tangensfunktion dem Winkel x den zugehörigen Tangentenabschnitt am Einheitskreis zuordnet, ordnet die Arkustangensfunktion umgekehrt dem Tangentenabschnitt am Einheitskreis den entsprechenden Winkel (im Bogenmaß) zu.

Der Funktionswert 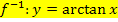entspricht somit einem Winkel am Einheitskreis.

Das Argument x der Arkustangensfunktion entspricht dem Tangentenabschnitt am Einheitskreis.

Übersicht:

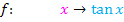
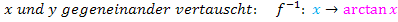
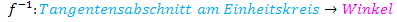
Der Winkel ist wieder im Bogenmaß. In der folgenden Abbildung ist der Winkel allerdings nicht als Bogen am Einheitskreis eingezeichnet, sondern zur einfacheren Darstellung als „normaler Winkel“. Betrachte nun die folgende Abbildung!

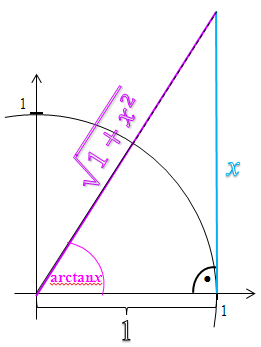
Abb. 4 Zur Erläuterung der Formel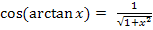

Hinweis zur Abbildung:Strenggenommen ist arctanx der Bogen auf dem Einheitskreis und nicht der Winkel im Gradmaß.

Man kann sich den Zusammenhang 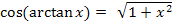jedoch besser erschließen, wenn man sich arctanx als „normalen Winkel“ vorstellt.

Wie kommt man jetzt auf 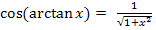? Wie oben schon erwähnt gilt:

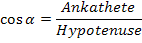
Dem Winkel 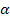entspricht in diesem Fall arctanx. Die Ankathete hat hier die Länge 1, also den Radius des Einheitskreises. Die Hypotenuse liegt gegenüber des rechten Winkels;die Hypotenuse, d.h. die Länge des schrägen lila Strichs ist noch unbekannt.

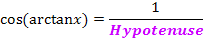
Damit leuchtet es ein, dass 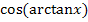1 / Hypotenuse entspricht. Wir berechnen die Länge der Hypotenuse mit Hilfe des Satzes von Pythagoras. Die eine Kathete ist 1;die andere Kathete ist x.

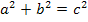
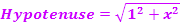
Somit gilt: .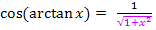

Nun ist dir hoffentlich klar, wieso dieser Zusammenhang gilt.

---