Schwierigere Variante der Substitution

Du willst wissen, wie man auf diese Formel kommt? Die Herleitung findest du bei:Wie berechnet man sin(arctanx),sin(arccosx), cos(arcsinx) und cos(arctanx)?

Nebenrechnung:

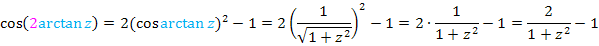
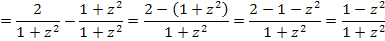
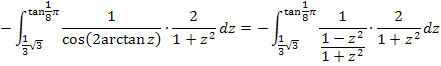
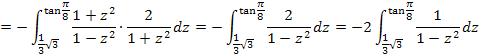
Nun haben wir endlich ein Integral vorliegen, das wir mit Hilfe einer Formel, die in der Formelsammlung steht, lösen können. Wir verwenden die folgende Formel: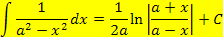

Mit a = 1 ergibt sich:

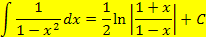
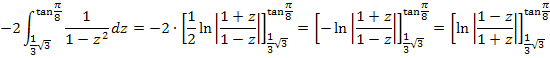
Die letzte Umformung hättest du nicht unbedingt machen müssen. (Du hättest auch vorher schon die Grenzen einsetzen können.) Falls dir der letzte Rechenschritt nicht klar ist, denke an das Logarithmus-Rechengesetz 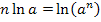. Daher gilt: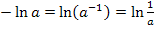

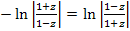Da für den Kehrwert von a steht, müsste dir nun klar sein, warum gilt.

Jetzt setzen wir die Grenzen ein.

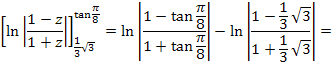
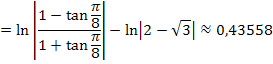
Nach der langwierigen Rechnung sind wir tatsächlich auf dasselbe Ergebnis gekommen, wie in Teilaufgabe 22a. Der soeben in 22b. gezeigte Rechenweg hat natürlich letztendlich auch zur Lösung geführt, aber es ist offensichtlich, dass die andere Substitution (vgl. 22a.) wesentlich schneller und einfacher zum Ergebnis führte.

Schlussbemerkung:

Das 22. Beispiel zeigte eindrucksvoll, wie schwierig manche Integrale zu lösen sein können. Manchmal geht es nämlich nicht einfacher und man ist schon froh, wenn man überhaupt einen Lösungsweg entdeckt hat, egal wie aufwendig er ist. Integrieren ist schlichtweg eine Kunst und verlangt viel mathematisches Fingerspitzengefühl und vor allem Erfahrung! Aber keine Sorge, eine Aufgabe wie Nr.22 musst du nicht alleine rechnen können! Es reicht, wenn du jeden einzelnen Schritt nachvollziehen konntest. Auch das ist schon schwer genug. Du solltest einfach ´mal sehen, wie man auch ganz schwere Integrale knacken kann. Die Kunst ist es, selbst auf solche Ideen zu kommen. Das bleibt dir als Schüler gottseidank erspart. Kein Mensch, auch kein Lehrer, erwartet so etwas von dir, solange du in die Schule gehst. An der Uni kann es dann allerdings anders aussehen;Ingenieurs- oder Mathematikstudenten müssen das schon können.

Graph der Funktion g

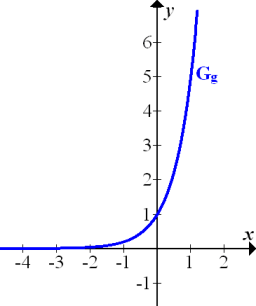
Abb.:Der Graph 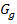der Funktion 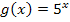nähert sich für 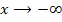asymptotisch an die x-Achse an, berührt sie aber nicht.

---