Schwierigere Variante der Substitution

Mit Hilfe des Logarithmus-Rechengesetzes 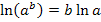lässt sich die ermittelte Stammfunktion auch in folgender Form schreiben:

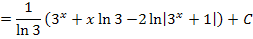
Die Betragsstriche können durch eine Klammer ersetzt werden, da der Term 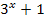sowieso immer positiv ist, egal was man für x einsetzt. ( 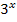ist schon positiv;dann ist 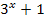erst recht positiv.)

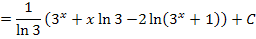
Damit sind wir fertig.

Nun wirst du dich vielleicht fragen, wie man denn selbst am besten darauf kommt, was 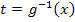sein muss, wenn es nicht schon angegeben ist. Tja, das verlangt entweder sehr viel Erfahrung oder schlichtweg Glück. Man kann nämlich tatsächlich jede beliebige umkehrbare Funktion als 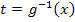verwenden. Erfreulicherweise gibt es aber manchmal nicht nur eine Substitution, die zur Lösung führt. Die nächste Beispielaufgabe lässt sich auch auf verschiedene Arten lösen. Sie dient aber vor allem als Extremfall, was den Schwierigkeitsgrad angeht. An der Abschlussaufgabe dieses Teiles wird deutlich werden, wie hoch die Ansprüche der Mathematik bei Integralen sein können.

Achtung:Das folgende Integral ist wirklich sehr schwierig (!!!) zu lösen. Du kannst es natürlich alleine versuchen. Doch sei bitte nicht enttäuscht, wenn du daran scheiterst. Selbstständig ohne Hilfe auf die Lösung zu kommen, ist für die meisten Schüler schlichtweg unmöglich. Daher wird es hier aber extra ganz ausführlich erklärt.

22. Bsp.:Für Könner oder Leute, die es werden wollen:Berechne !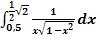

a.) Mit der Substitution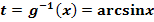

b.) Mit der Substitution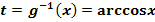

Lösung:

Zu 22a.)

1. Schritt:Substitution 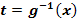und nach x auflösen

Laut Angabe: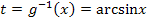

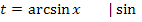
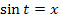
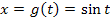
2. Schritt: 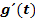bilden

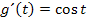
3. Schritt:dx gleich 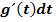setzen

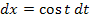
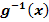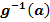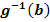4. Schritt:Ursprünglichen Grenzen a und b in einsetzen. Das ergibt die neuen Grenzen und bezüglich der neuen Variablen t.

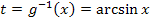
Ursprüngliche Grenzen:0,5 (untere Grenze) und 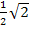(obere Grenze)

Neue untere Grenze: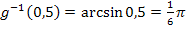

Neue obere Grenze:

5. Schritt:Ersetze im Integranden (d.h. in der zu integrierenden Funktion) jedes x durch 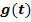und versuche das Integral mit den neuen Grenzen 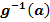und 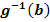zu lösen.

Subst.: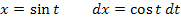

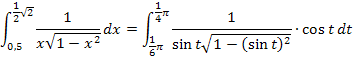
Nun verwenden wir den trigonometrischen Pythagoras, d.h. den folgenden Zusammenhang:

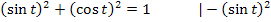
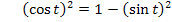
Wir können somit statt dem Ausdruck 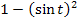, der beim Integranden im Nenner unter der Wurzel steht, einfach 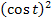schreiben. Dadurch vereinfacht sich das Integral erheblich.

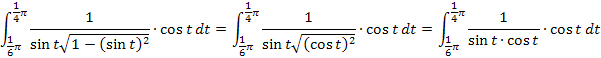
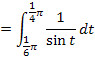
Das neue Integral ist zwar schon viel übersichtlicher, doch leicht zu lösen ist es leider nicht.

---