Schwierigere Variante der Substitution

Der Integrand ist offensichtlich ein Produkt eines Polynoms (1. Grades) und einer leicht integrierbaren Funktion. Vergleiche dazu 7. Bsp.! Das neue Integral lässt sich somit lösen. Die Substitution 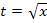war sinnvoll.

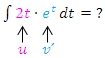
In einer Nebenrechnung bilden wir vorweg u´ und v.

Das kannst du bestimmt auch alleine. Zu deiner Kontrolle hier die Zwischenergebnisse:

Nun setzen wir alles in die Formel der partiellen Integration ein.

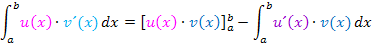
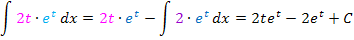
Als nächstes ersetzen wir noch jedes t durch 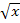. (Rücksubstitution)

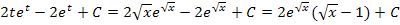
Hier noch einmal die komplette Rechnung:

Substitution: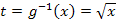

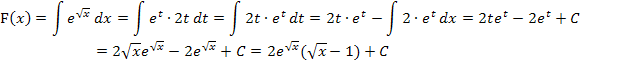
Da in der Aufgabe nur nach einer Stammfunktion zu 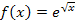gefragt ist, kann für C eine beliebige Zahl eingesetzt werden, also auch die Zahl 0. Dann fällt die Integrationskonstante C praktisch weg. Du kannst natürlich genauso gut eine andere Zahl für C wählen oder „+ C “ einfach stehen lassen.

An diesem Beispiel konntest du sehen, wie die Substitutionsmethode (schwierige Variante) auch bei unbestimmten Integralen funktioniert. Es wird dabei am Schluss jedes t wieder durch die gewählte Funktion 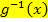ersetzt, damit kein t, sondern nur noch die ursprüngliche Variable x in der Stammfunktion F vorkommt.

Theoretisch lassen sich auch bestimmte Integrale nach diesem Prinzip lösen. Dann lässt man die Grenzen unverändert, muss aber zum Schluss die Rücksubstitution durchführen, bevor die Grenzen eingesetzt werden. Die ursprünglichen Grenzen beziehen sich schließlich auf die ursprüngliche Variable x und dürfen daher nur für x eingesetzt werden, nicht aber für t.

Im letzten Beispiel war es recht leicht darauf zu kommen, wie substituiert werden musste. Das ist leider nicht immer der Fall, so auch in der nächsten Beispielaufgabe. Die nächste Aufgabe ist aber nicht so schwer, dass man gar nicht selbst darauf kommen kann. Also versuch´s doch erst einmal alleine, bevor du dir die Lösung ansiehst!

21. Bsp.:Berechne mittels geeigneter Substitution !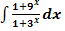

Lösung:

Das Problem an dieser Aufgabe ist es herauszufinden, wie man geschickt substituiert. Nach einer kleinen Umformung des Integranden, müsstest du alleine darauf kommen. Statt 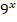schreiben wir 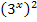. Bei dieser Umformung wurde das Potenzgesetz 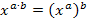quasi „rückwärts“ angewendet. Nicht klar? Ok, dann ganz ausführlich: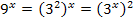

Damit gilt:

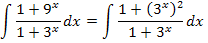
Was wird man hier wohl gleich t setzen?

Na klar! Es bietet sich die folgende Substitution an:

Wir lösen nach x auf.

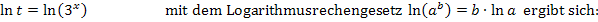
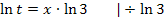
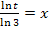
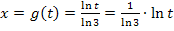
Nun leiten wir 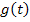nach t ab. Der Ausdruck 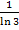wird beim Ableiten einfach abgeschrieben, da es sich um eine multiplikative Konstante handelt, also eine Zahl ohne Variable, die mit etwas multipliziert wird.

---