Schwierigere Variante der Substitution

Der Knackpunkt ist schließlich, ob sich das neue Integral leichter berechnen lässt als das alte. (Hier wird das natürlich der Fall sein, denn sonst wäre die Substitution nicht so verlangt worden.)

Wir ersetzen im Integranden also jedes x durch 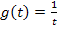und dx durch 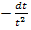. Außerdem verwenden wir natürlich die neuen Grenzen und versuchen danach zu integrieren.

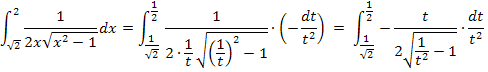
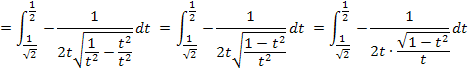
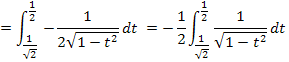
Mit der Formel 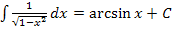lässt sich das neue Integral leicht berechnen. Die Substitution 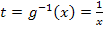hat also ihren Zweck erfüllt. Ab jetzt dürfte sich kein Problem mehr ergeben. Rechne ab hier doch gleich alleine weiter und vergleiche erst dann mit der folgenden Lösung!

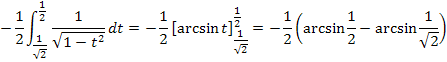
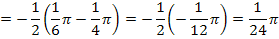
Fertig!

Auch bei unbestimmten Integralen kann die Integration mittels Substitution angewendet werden. Wie das geht, wird im nächsten Beispiel gezeigt.

20. Bsp.:Ermittle eine Stammfunktion zu !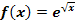

Lösung:

Um eine Stammfunktion von 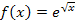zu finden, muss das folgende unbestimmte Integral gelöst werden:

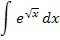
Wir verwenden die Substitutionsmethode (schwierige Variante). Dabei gehen wir wieder Schritt für Schritt nach obiger Anleitung vor.

1. Schritt:Geeignete Substitution 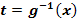durchführen und nach x auflösen;das ergibt .

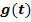Es bietet sich die folgende Substitution an:

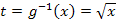
Die Wurzelfunktion ist eine umkehrbare Funktion. Die ist Voraussetzung bei dieser Methode, da man ansonsten nicht eindeutig nach x auflösen könnte. Genau das müssen wir aber als nächstes machen.

Auflösen nach x ergibt .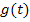

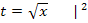
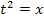
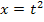
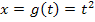
2. Schritt: 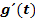bilden

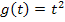
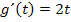
3. Schritt:dx gleich 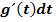setzen

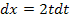
4. Schritt:Ursprünglichen Grenzen a und b in 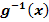einsetzen.

Dieser Schritt entfällt, da wir ja gar keine Grenzen haben, die wir einsetzen könnten. Es handelt sich hier schließlich um ein unbestimmtes Integral. Stattdessen müssen wir hier nach erfolgreicher Integration jedes t letztendlich wieder durch 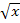ersetzen. Vergleiche dazu die im 1. Schritt durchgeführte Substitution: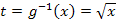

5. Schritt:Ersetze im Integranden (d.h. in der zu integrierenden Funktion) jedes x durch 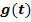und versuche das Integral zu lösen.

Wir ersetzen im Integranden also jedes x durch 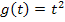und dx durch 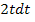. Dann versuchen wir zu integrieren.

Jetzt wird es wieder spannend. Klappt die Integration des neuen Integrals?

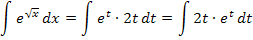
Dieses neue Integral packen wir mit einer partiellen Integration (Typ „Abräumen“). Die Substitution hat also funktioniert!

---