Einfachere Variante der Integration durch Substitution

Lösung:

Um eine Stammfunktion F(x) zu finden, muss das folgende unbestimmte Integral berechnet werden:

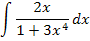
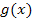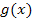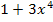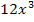Es kann mittels Substitution gelöst werden. Die Frage ist nur, wie bzw. t gewählt werden muss. Denn kompletten Nenner als aufzufassen, bringt nichts, denn die Ableitung von ist ;sie steht nicht da. (Im Zähler steht schließlich kein 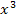, sondern 2x. Das ist kein Vielfaches der Ableitung des Nenners. Die x-Potenz, die da steht, muss bei dieser Methode wirklich mit der Ableitung von 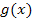übereinstimmen.) Wir müssen uns etwas anderes einfallen lassen, um diese Integral zu lösen.

Wir formen um:

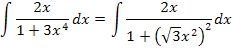
Nun erkennt man besser, dass 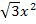gleich 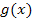ist. Die Ableitung von 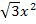ist 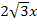;im Zähler steht 2x, also ein Vielfaches davon. Das passt schon ´mal. Also los geht´s!

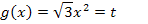
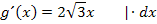
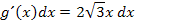
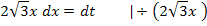
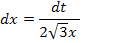
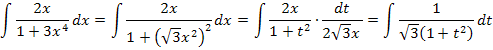
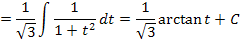
Nun folgt noch die Rücksubstitution;wir ersetzen t wieder durch .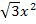

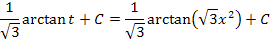
Wer mag, kann den Nenner von 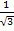noch rational machen. Es wird dazu mit 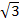erweitert.

Nebenrechnung: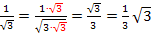

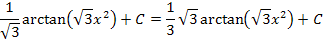
Fertig!

Wie du an diesem Beispiel sehen konntest, ist es oft gar nicht so einfach zu erkennen, wie man substituieren muss. Integrieren lernt man nur durch Erfahrung. Nur wenn man schon ähnliche Aufgaben gesehen hat, kommt man später selbst auf die richtige Idee.

In der Formelsammlung findest du noch weitere Integrale, die du verwenden kannst. Hier die wichtigsten davon:

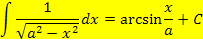
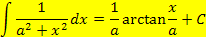
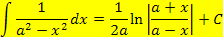
Mit Hilfe der gezeigten Integrale lassen sich auch Integrale der Form 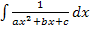und 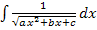lösen. Man muss vorher einen Teil des Nenners zu einer binomischen Formel umformen. Wie das geht, wird im nächsten Beispiel vorgeführt. Das musst du aber nur dann können, wenn ihr in der Schule ähnliche Integrale berechnet habt.

18. Bsp.:Berechne !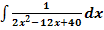

Lösung:

Um dieses Integral zu lösen, müssen wir etwas tiefer in die mathematische Trickkiste greifen. Zuerst klammern wir diejenige Zahl aus, die im Nenner vor 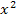steht.

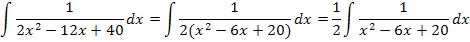
Nun führen wir im Nenner eine quadratische Ergänzung durch, um künstlich eine binomische Formel herzustellen. (Zur Erinnerung:Man nimmt die Zahl vor dem x, halbiert sie und quadriert sie. Das Ergebnis wird dann zuerst addiert und danach gleich wieder subtrahiert. Das stimmt aber wirklich nur dann, wenn vor 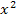keine Zahl steht;daher war das vorherige Ausklammern der Zahl 2 nötig.)

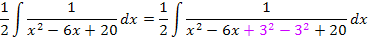
Nun formen wir die binomische Formel um.

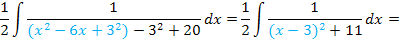
Wir stellen die Reihenfolge um und schreiben statt 11 einfach 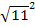. Das machen wir, damit wir nach der Substitution mit der Formel 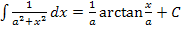arbeiten können.

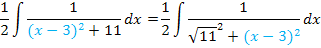
Jetzt müssen wir nur noch eine geeignete Substitution durchführen. Überlege dir selbst, wie hier substituiert werden muss!

---