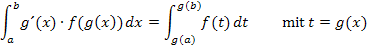Einfachere Variante der Integration durch Substitution
)
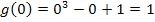
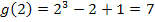
5. Schritt:Berechnung des Integrals
Die neue untere Grenze ist 1, die neue obere Grenze ist 7. Nun können wir endlich das Integral 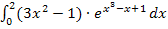 ausrechnen. Statt dem Exponenten
ausrechnen. Statt dem Exponenten 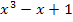 schreiben wir t und statt dx schreiben wir
schreiben wir t und statt dx schreiben wir 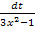 .
.
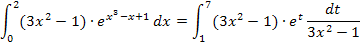
Der Ausdruck 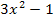 lässt sich dabei komplett herauskürzen, so dass letztendlich kein x mehr im neuen Integral vorkommt. Das ist auch der Grund, warum die Ableitung
lässt sich dabei komplett herauskürzen, so dass letztendlich kein x mehr im neuen Integral vorkommt. Das ist auch der Grund, warum die Ableitung 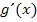 oder ein Vielfaches davon bereits dastehen muss. Ansonsten könnte man nicht entsprechend kürzen und es verbliebe neben der neuen Variablen t auch noch die alte Variable x. Das würde nicht funktionieren. x muss sich komplett herauskürzen lassen, sonst klappt diese Methode der Integration nicht! Das ist jedoch immer der Fall, wenn
oder ein Vielfaches davon bereits dastehen muss. Ansonsten könnte man nicht entsprechend kürzen und es verbliebe neben der neuen Variablen t auch noch die alte Variable x. Das würde nicht funktionieren. x muss sich komplett herauskürzen lassen, sonst klappt diese Methode der Integration nicht! Das ist jedoch immer der Fall, wenn 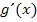 ein Teil des Integranden ist. Daher musst du bei dieser Methode
ein Teil des Integranden ist. Daher musst du bei dieser Methode 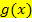 immer von Anfang an so wählen, dass die Ableitung davon schon im Integranden steckt.
immer von Anfang an so wählen, dass die Ableitung davon schon im Integranden steckt.
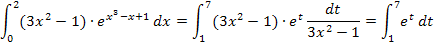
Nun liegt ein Integral vor, das nur noch t, aber kein x mehr enthält;es ist leicht zu berechnen. Daran siehst du, dass die Substitution 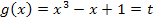 sinnvoll war. Bei der Integration mittels Substitution versucht man durch geeignete Substitution ein neues, deutlich einfacheres Integral mit der anderen Variable t zu erschaffen. Hier ist uns das durch die oben gezeigte Substitution gelungen. Wir müssen nur noch das neue Integral ausrechnen. Doch das dürfte kein Problem mehr für dich darstellen. Rechne es doch gleich alleine aus!
sinnvoll war. Bei der Integration mittels Substitution versucht man durch geeignete Substitution ein neues, deutlich einfacheres Integral mit der anderen Variable t zu erschaffen. Hier ist uns das durch die oben gezeigte Substitution gelungen. Wir müssen nur noch das neue Integral ausrechnen. Doch das dürfte kein Problem mehr für dich darstellen. Rechne es doch gleich alleine aus!
Du solltest auf folgendes Ergebnis gekommen sein:
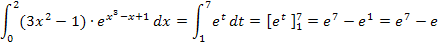
Hinweis:Dieses Integral hätte auch mit der Formel 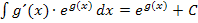 berechnet werden können.
berechnet werden können.
| Zusammenfassung: Integration durch Substitution (einfache Variante)
Integrale der Form 1. Schritt:Geeignete Substitution durchführen Wähle 2. Schritt:Bilde
3. Schritt:Setze den erhaltenen Ausdruck gleich dt und löse nach dx auf.
4. Schritt:Berechnung der neuen Grenzen Setze die ursprünglichen Grenzen a und b in die Funktion Neue untere Grenze: Neue obere Grenze: 5. Schritt:Berechnung des Integrals Verwende die neuen Grenzen an statt der ursprünglichen Grenzen, ersetze die innere Funktion
|
Nun ein Beispiel eines unbestimmten Integrals, das mittels Substitution (einfache Variante) gelöst werden kann.

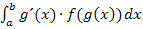 können auf folgende Art und Weise gelöst werden:
können auf folgende Art und Weise gelöst werden: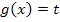 so, dass die Ableitung
so, dass die Ableitung 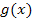 so wählen, dass die Ableitung
so wählen, dass die Ableitung 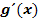 und erweitere mit dem Ausdruck dx.
und erweitere mit dem Ausdruck dx.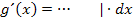
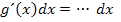
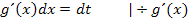
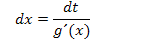
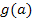
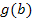
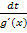 . Kürze
. Kürze