2a. Partielle Integration
Hier noch einmal die Formel: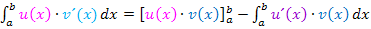 
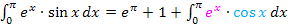
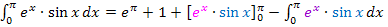
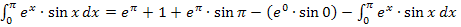
Mit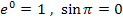 
und 
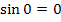ergibt sich:
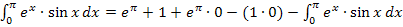
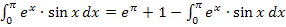
Jetzt kommt der entscheidende Schritt:Durch die zweite partielle Integration hat sich ein Ausdruck ergeben, der wieder das ursprüngliche Integral enthält.
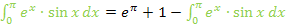
Wir haben nun eine Gleichung vor uns, die das gesuchte Integral auf der linken und rechten Seite enthält. Das auf der rechten Seite stehende Integral bringen wir nun einfach auf die linke Seite der Gleichung. Wir wollen die Gleichung nämlich einfach nach dem Integral auflösen.
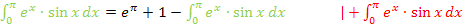
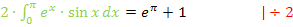
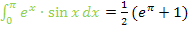
Damit ist das Integral gelöst!
Wer will, kann den Faktor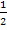 
noch in die Klammer hinein multiplizieren. Dann ist man aber wirklich fertig.
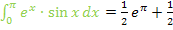
Der Trick des Typ „Phönix“ besteht also darin, dass man durch geschickte partielle Integration(en) einen Ausdruck erzeugt, der wieder das ursprüngliche Integral oder ein Vielfaches davon enthält. Dann liegt eine Gleichung vor, die durch herkömmliches Umstellen nach dem Integral aufgelöst werden kann.
Dieser Typ funktioniert natürlich nur dann, wenn man durch partielle Integration das ursprüngliche Integral wieder erzeugen kann. Dies ist z. B. bei Integralen von Produkten möglich, welche die Faktoren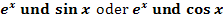 
enthalten, bzw. auch bei den Integralen von 
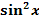oder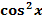 
.
Bei der Integration nach Typ „Phönix“ braucht man, wie oben am Beispiel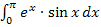 
gezeigt, in der Regel zwei partielle Integrationen, um das ursprüngliche Integral wieder zu erzeugen. Es gibt aber auch Ausnahmen, wobei nur eine partielle Integration und eine kleine Umformung nötig ist. Das ist beispielsweise bei 
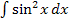und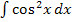 
der Fall. Wie das funktioniert, kannst du im nächsten Beispiel sehen.
14. Bsp.:Es soll das folgende Integral berechnet werden:
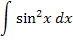
An Stelle von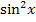 
kann natürlich auch 
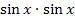geschrieben werden. Dann liegt ein Produkt vor;wir können die partielle Integration anwenden. Den einen Sinus betrachten wir als u, den anderen als v´.
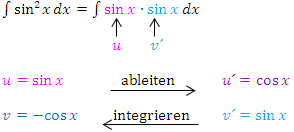
Hier noch einmal die Formel: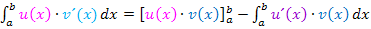
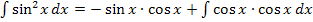
Nun machen wir keine zweite partielle Integration. Du kannst es selbst ´mal ausprobieren, was passiert, wenn man doch eine zweite partielle Integration mit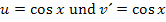 
durchführt. Dann wirst du feststellen, dass sich letztendlich 
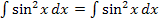ergibt. Dies ist natürlich wahr, doch bringt es uns natürlich nicht weiter.
Was also stattdessen tun? Irgendwie müssen wir wieder auf das ursprüngliche Integral kommen, aber so dass nicht alles andere dabei wegfällt. Statt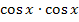 
schreiben wir erst einmal 
.
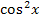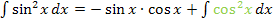
Von 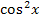müssen wir jetzt irgendwie wieder auf einen Ausdruck mit 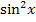kommen.
