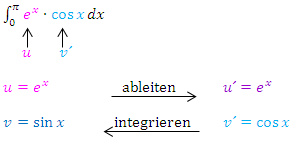
2a. Partielle Integration
Wir wählen daher für die partielle Integration:

Einsetzen in die Formel der partiellen Integration:
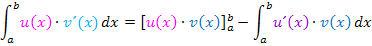
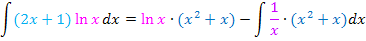
Der vordere Teil ist bereits fertig, der hintere Teil enthält noch ein Integral. Dieses neue Integral muss noch ausgerechnet werden. Es lässt sich leicht berechnen, wenn man den neuen Integrand ausmultipliziert.
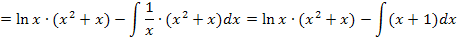
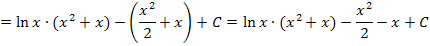
An diesem Beispiel konntest du sehen, dass es geschickt ist, eine auftretende ln-Funktion bei der partiellen Integration immer mit u zu bezeichnen.
3. Typ „Phönix“
Diese Integrationsmethode eignet sich hauptsächlich für Integrale von Produkten, welche die Faktoren 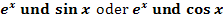 enthalten, bzw. auch bei den Integralen von
enthalten, bzw. auch bei den Integralen von 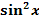 oder
oder 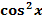 .
.
Typ „Phönix“ ist wirklich trickreich. Man versucht dabei mit Hilfe der partiellen Integration wieder auf das ursprüngliche Integral bzw. ein Vielfaches davon zu kommen. Das ursprüngliche Integral entsteht wie der Phönix aus seiner Asche. (Der Name kommt aus der Mythologie, von dem sagenhaften Vogel Phönix, der immer wieder aus seiner Asche entsteht.) Dadurch ergibt sich eine Gleichung, die letztendlich nach dem gesuchten Integral aufgelöst werden kann.
Am besten lässt sich das an Hand eines konkreten Beispiels erklären.
13. Bsp.:Berechne das folgende Integral.
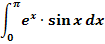
Lösung:
In diesem Fall spielt es keine Rolle, welchen Faktor des Produkts man mit 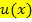 und welchen man
und welchen man 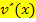 nennt. Es ist also egal, ob man
nennt. Es ist also egal, ob man 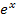 gleich
gleich 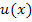 und
und 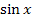 gleich
gleich 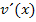 setzt oder umgekehrt
setzt oder umgekehrt 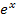 gleich
gleich 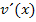 und
und 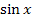 gleich
gleich 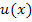 . Beides führt letztendlich zur Lösung des Integrals. (Warum das so ist, wird dir sicher nachher noch klar werden. Schaue dir erst einmal die folgende Rechnung an. Danach kannst du selbst die andere Variante versuchen. Du wirst sehen, dass auch dies funktioniert.)
. Beides führt letztendlich zur Lösung des Integrals. (Warum das so ist, wird dir sicher nachher noch klar werden. Schaue dir erst einmal die folgende Rechnung an. Danach kannst du selbst die andere Variante versuchen. Du wirst sehen, dass auch dies funktioniert.)
Wir entscheiden uns hier für die erstere Variante und legen folgendes fest:
1. Partielle Integration:
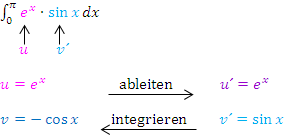
Wir setzen in die Formel 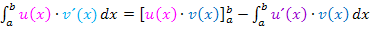 ein.
ein.
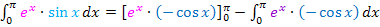
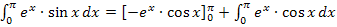
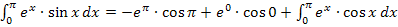
Mit 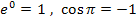 und
und 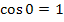 ergibt sich:
ergibt sich:
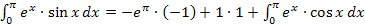
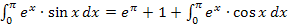
Dem neuen Integral rücken wir mit einer zweiten partiellen Integration zu Leibe. Dabei gilt es zu beachten, dass die e-Funktion, wie schon bei der ersten partiellen Integration, 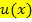 genannt wird.
genannt wird.
Wenn du 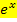 bei der ersten partiellen Integration u nennst, musst du das beim Typ „Phönix“ unbedingt auch bei der zweiten partiellen Integration so machen. (Hätte man die e-Funktion bei der ersten partiellen Integration als v´ angesehen, müsste man
bei der ersten partiellen Integration u nennst, musst du das beim Typ „Phönix“ unbedingt auch bei der zweiten partiellen Integration so machen. (Hätte man die e-Funktion bei der ersten partiellen Integration als v´ angesehen, müsste man 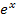 auch bei der zweiten partiellen Integration wieder v´ nennen.)
auch bei der zweiten partiellen Integration wieder v´ nennen.)
2. Partielle Integration: