2a. Partielle Integration
Damit du das besser verstehen kannst, machen wir das an einem konkreten Beispiel.
11. Bsp.:Berechne das unbestimmte Integral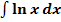 
.
Lösung:
Das gesuchte Integral steht zwar in der Formelsammlung bzw. auf der Merkhilfe, doch wollen wir es hier selbst lösen, also ohne Verwendung der Formelsammlung oder Merkhilfe. An diesem Beispiel kann man das Prinzip der Methode „Faktor 1“ nämlich besonders schön erklären.
Die Funktion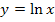 
lässt sich leicht ableiten;bekanntlich gilt:
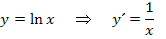
Wie kann man nun 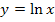integrieren?
Wir multiplizieren mit der Zahl 1. Dann liegt praktisch ein Produkt vor und es lässt sich eine partielle Integration durchführen. Die Zahl 1 fassen wir als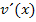 
auf, die ln-Funktion entsprechend als 
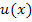. Die ln-Funktion muss dann abgeleitet und die Zahl 1 integriert werden.
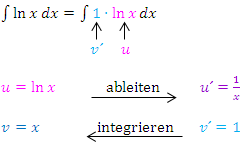
Wir setzen in die Formel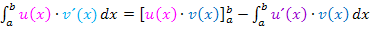 
ein. Da hier ein unbestimmtes Integral vorliegt, lassen wir einfach die Grenzen a und b bei der Formel weg. Die eckigen Klammern, die symbolisieren, dass der Ausdruck innerhalb bereits integriert wurde, braucht man beim unbestimmten Integral auch nicht. Trotzdem ist der vordere Teil bereits integriert;nur den hinteren Teil muss man in einem zweiten Schritt noch integrieren. Am Schluss müssen wir außerdem noch „+ C“ dazu schreiben.
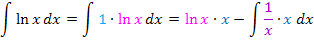
Nun lässt sich im neu entstandenen Integral x kürzen. So entsteht ein ganz leicht zu berechnendes Integral.
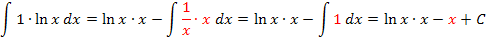
Fertig!
Allgemein lässt sich feststellen, dass der Typ „Faktor 1“ der partiellen Integration immer dann funktioniert, wenn man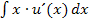 
lösen kann. Warum? Schauen wir das genauer an.
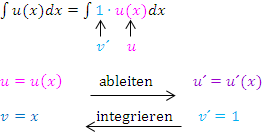
Wir setzen in die Formel 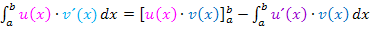ein.
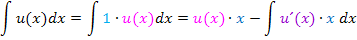
Nun muss noch das Integral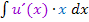 
berechnet werden. Nur wenn das möglich ist, bringt die Methode „Faktor 1“ etwas. Aber das kann man sich schließlich leicht vorher überlegen. Dieser Typ der partiellen Integration ist allerdings recht selten.
Tipp:Wenn du eine partielle Integration (nicht nur Typ „Faktor 1“) bei einem Integral durchführen willst, in dem unter anderem lnx vorkommt, solltest du immer die ln-Funktion als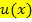 
wählen. Die ln-Funktion wird bei der partiellen Integration generell abgeleitet und der andere Faktor entsprechend integriert.
12. Bsp.:
Berechne das folgende unbestimmte Integral!
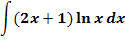
Lösung:
Der Integrand ist ein Produkt, das in beiden Faktoren die Variable x enthält. Es bietet sich daher die partielle Integration an. Der eine Faktor des Produkts ist die ln-Funktion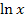 
;diesen Faktor wollen wir bei der partiellen Integration ableiten.
