2a. Partielle Integration
Du denkst jetzt wahrscheinlich, es liegt hier gar kein Integral der Form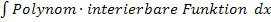 
vor. Die partielle Integration Typ „Abräumen“ führt aber dennoch zur Lösung. Bloßwie?
Überlege dir Folgendes:Mit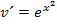 
klappt es nicht, aber anders sähe es dagegen bei 
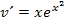aus, weil dies schon fast eine Funktion der Form 
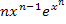ist. Darauf könnte die Integrationsregel 
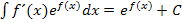angewendet werden. Auf diese Aufgabe bezogen heißt das, die Funktion 
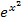lässt sich alleine nicht integrieren, aber die Funktion 
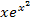schon, da sie bis auf eine multiplikative Konstante die Form 
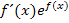besitzt. Das Integral 
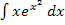können wir leicht lösen:Wir bekommen exakt die Ableitung des Exponenten, also den Ausdruck 2x, indem wir die Konstante 
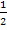vor das Integral schreiben.
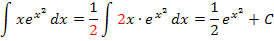
Was hat das nun mit der Lösung des Integrals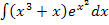 
zu tun? Ganz einfach, wir klammern x aus und schon können wir das Integral mittels partieller Integration lösen!
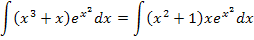
Wir wählen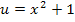 
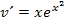und . Damit klappt die partielle Integration.
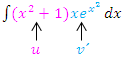
Partielle Integration:
Wir setzen in die Formel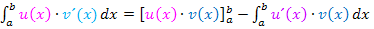 
ein.
Da es sich hier um ein unbestimmtes Integral, also um ein Integral ohne Grenzen handelt, fallen in diesem Fall die Grenzen a und b weg. Dafür müssen wir aber am Ende der Rechnung „+ C“ dazu schreiben.
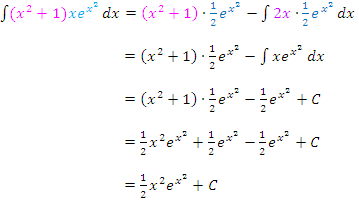
Fertig!
An diesem Beispiel war schön zu sehen, dass die eigentliche Schwierigkeit gar nicht in der Rechnung lag. Das Problem lag vielmehr darin, auf die zündende Idee zu kommen. Wer nicht die Idee hatte x auszuklammern und 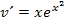zu wählen, wird nicht auf die Lösung des Integrals gekommen sein.
Falls du das letzte Integral nicht alleine lösen konntest, bitte jetzt nicht sofort aufgeben und alles hinschmeißen frei nach dem Motto:Das lerne ich nie. Da komme ich niemals alleine drauf! Diese Aufgabe war wirklich nicht einfach. Doch das hat alles nur mit Erfahrung und Übung zu tun. Gerade deshalb erst recht weiter zum nächsten Typ und den nächsten Aufgabenbeispielen!
2. Typ „Faktor 1“
Die partielle Integration kann nicht nur bei der Integration von Produkten eingesetzt werden. Ein Trick ermöglicht es in besonderen Fällen auch Funktionen zu integrieren, die keine Produkte sind. Man schreibt einfach den Faktor 1 vor die zu integrierende Funktion. Die Zahl 1 betrachten wir dann als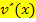 
und die eigentlich zu integrierende Funktion als 
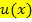. Diese Methode eignet sich vor allem für Funktionen, die sich zwar schlecht integrieren, aber leicht ableiten lassen. Genau genommen funktioniert sie bei der Integration aller Funktionen, deren Ableitung mit x multipliziert ein lösbares Integral ergeben.
