2a. Partielle Integration

(Unten in Rot geschrieben) Dieses Minuszeichen muss sich nach der dritten partiellen Integration auf den gesamten nachfolgenden Ausdruck beziehen. Daher muss eine Klammer um den gesamten Ausdruck gesetzt werden, der sich nun durch die partielle Integration ergibt. (Große schwarze Klammer in der übernächsten Zeile)

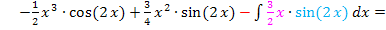
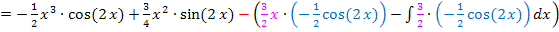
Nun lösen wir die Klammern auf und vereinfachen so weit möglich. Das ergibt:

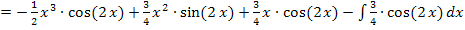
Jetzt muss noch das verbliebene Integral berechnet werden;das ist aber kein Problem. Die multiplikative Konstante 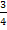kann vor das Integral gezogen werden. 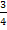wird praktisch abgeschrieben, wenn man integriert. Eine Stammfunktion von 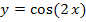haben wir bei der zweiten partiellen Integration schon ermittelt;es gilt: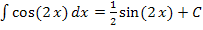

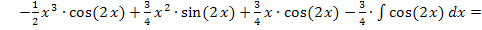
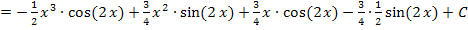
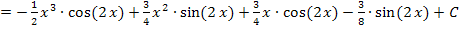
Hinweis:Es ist völlig ausreichend hinter den gesamten Ausdruck einmal „+ C“ zu schreiben. Es muss nicht bei jedem einzelnen Integrationsschritt 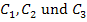verwendet werden. Da es sich sowieso um unbekannte Konstanten handelt, kann 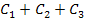zu einer Konstante C zusammengefasst werden.

Wer mag, kann das Ergebnis noch weiter vereinfachen.

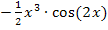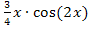Aus den Ausdrücken und kann beispielsweise 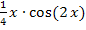ausgeklammert werden. Aus den Ausdrücken 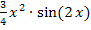und 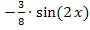kann zum Beispiel 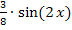ausgeklammert werden.

Zur Erinnerung:Ein Bruch wird ausgeklammert, indem man durch ihn teilt, d.h. mit seinem Kehrwert multipliziert.

Als erstes ordnen wir nach Termen mit Kosinus und Termen mit Sinus.

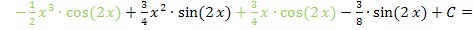
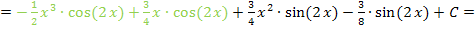
Nun wird jeweils einzeln bei den ersten Termen und bei den beiden hinteren Termen ausgeklammert.

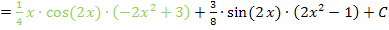
Die Brüche hätte man nicht unbedingt ausklammern müssen, aber dadurch erhält man in den Klammern nur noch ganze Zahlen, was eben schöner aussieht.

So, endlich fertig!

Puh, das war wirklich eine lange Rechnung. Drei partielle Integrationen nacheinander sind echt sehr viel Arbeit. Nun leuchtet es dir auch bestimmt ein, dass man den Typ „Abräumen“ nur dann anwendet, wenn es sich ursprünglich bei 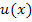um ein Polynom höchstens dritten Grades handelt.

Manchmal geht es aber auch bei einem Polynom dritten Grades ein wenig schneller, das zeigt uns das nächste Beispiel. Versuche es zuerst alleine, obwohl es nicht ganz leicht ist auf die zündende Idee zu kommen, wie sich dieses Integral knacken lässt.

10. Bsp.:

Berechne das folgende Integral!

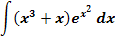
Lösung:

Das Problem besteht darin, dass sich eine Funktion der Form 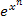alleine nicht integrieren lässt. Wenn du 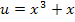und 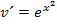wählst, kannst du v nicht ermitteln, weil sich 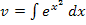nicht berechnen lässt.

---