2a. Partielle Integration
Bereits die erste Ableitung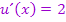 
enthält kein x mehr.
Das neue Integral hat bei der partiellen Integration immer die Form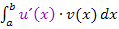 
. Da die Ableitung 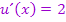kein x mehr enthält, ist das neue Integral wesentlich einfacher zu lösen. Wie du weißt, bleiben multiplikative Konstanten (d.h. Zahlen ohne x, die multipliziert werden) beim Integrieren einfach stehen. Die Ableitung 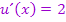ist bei dem neuen Integral = 
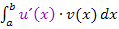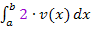nichts anderes als eine multiplikative Konstante. Daher ist das neue Integral einfacher als das ursprüngliche. Man musste nur einmal ableiten und schon war das Polynom „abgeräumt“.
Dieses Verfahren funktioniert entsprechend, wenn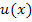 
ein beliebiges Polynom ersten Grades ist. Den anderen Faktor 
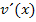muss man natürlich integrieren können, sonst klappt der Typ „Abräumen“ nicht.
Ist der Faktor 
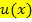ein Polynom ersten Grades genügt eine partielle Integration.
Bloß, was macht man, wenn 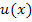ein Polynom zweiten oder dritten Grades ist?
Dann muss die partielle Integration mehrfach nacheinander durchgeführt werden.
Ist das Polynom 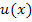ein Polynom zweiten Grades, muss man zweimal ableiten, bis es komplett abgeräumt ist und nur noch eine Konstante/Zahl übrig bleibt. Man führt die partielle Integration einfach zweimal nacheinander durch.
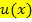Ist ein Polynom zweiten Grades braucht man zwei partielle Integrationen.
Bei einem Polynom dritten Grades, das mit einer integrierbaren Funktion multipliziert ist, muss dreimal abgeleitet werden, bis das Polynom durch das Ableiten „abgeräumt“ ist. Nach drei partiellen Integrationen tritt kein Polynom mehr im letztendlich entstehenden Integral auf. Diese dritte neue Integral kann dann leicht auf herkömmlichen Weg berechnet werden.
Ist 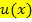ein Polynom dritten Grades braucht man drei partielle Integrationen.
Der Grad des Polynoms gibt somit an, wie oft die partielle Integration durchgeführt werden muss. Man braucht also immer n partielle Integrationen, wenn das Polynom, das mit einer integrierbaren Funktion multipliziert wird, den Grad n besitzt.
Ist 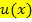ein Polynom n-ten Grades braucht man n partielle Integrationen.
Ist 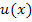ein Polynom vierten Grades bräuchte man folglich vier partielle Integrationen. Das wäre aber mit extrem viel Rechenaufwand verbunden. Daher empfiehlt sich die partielle Integration Typ „Abräumen“ dann nicht mehr. Ist das Polynom höher als dritten Grades solltest du dir Gedanken über einen anderen Lösungsweg machen;der Typ „Abräumen“ ist es dann sicherlich nicht. (Aufgaben mit mehr als drei partiellen Integrationen nacheinander wird dir kein vernünftiger Lehrer stellen.)
Schauen wir uns nun einige konkrete Beispiele an, bei denen mehrere partielle Integrationen nacheinander nötig sind.
