2a. Partielle Integration

Wir stellen nach 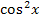um und setzen nachher das Ergebnis in unser Integral ein.

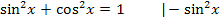
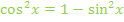
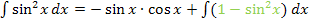
Nun teilen wir das Integral auf;bei Differenzen und Summen ist das schließlich erlaubt. (Bei Produkten und Quotienten natürlich nicht!)

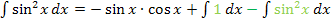
Endlich haben wir unser ursprünglich gesuchtes Integral wieder vorliegen. Wir müssen nur noch 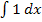berechnen und die Gleichung nach dem Integral auflösen.

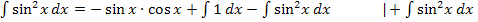
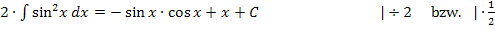
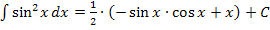
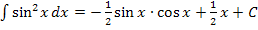
Hinweis:Streng genommen hätten wir statt „+ C“ eigentlich „+ 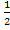C“ schreiben müssen. Doch da C sowieso eine unbekannte Konstante ist, ist das egal. Ganz mathematisch korrekt würde man folgendermaßen vorgehen:

Zuerst nennt man die Integrationskonstante nicht C, sondern C*.

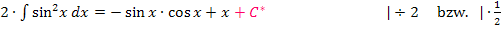
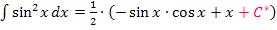
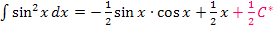
Mit 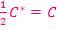ergibt sich letztendlich das Ergebnis von oben:

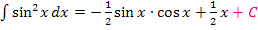
Den Umweg über 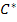musst du aber nicht unbedingt machen;du kannst es direkt mit „+ C“ schreiben, wie oben schon gezeigt.

Der entscheidende Schritt war hier die Verwendung des trigonometrischen Pythagoras, d.h. die Formel 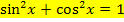. Merke dir diesen Trick gut! Zur Übung solltest du nun gleich versuchen das Integral 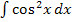zu lösen. Das funktioniert nach demselben Prinzip.

---