1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen

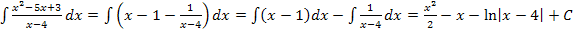
Auch unser erstes Beispiel 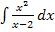kann mit Hilfe einer Polynomdivision berechnet werden. Man muss also nicht unbedingt im Zähler ergänzen. Versuche doch gleich ´mal alleine das Integral 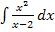mit Hilfe einer vorherigen Polynomdivision zu berechnen!

Du solltest auf folgende Lösung gekommen sein:

Polynomdivision:

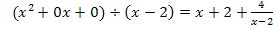
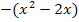
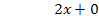
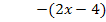
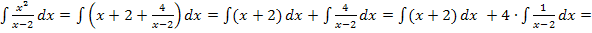
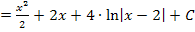
Dasselbe Ergebnis haben wir auch oben mit der anderen Methode erhalten.

Dies waren die wichtigsten Fälle, die sich letztendlich mit der Formel 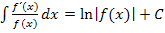lösen lassen.

Zusammenfassend lässt sich sagen: Die Regel kann angewendet werden, wenn der Zähler des zu integrierenden Bruchs genau der Ableitung des Nenners entspricht der Zähler des zu integrierenden Bruchs einem Vielfachen der Ableitung des Nenners entspricht; dann muss zum Ausgleich allerdings ein entsprechender Faktor vor das Integral geschrieben werden. (Den jeweiligen Faktor bekommst du heraus, indem du den ursprünglichen Zähler durch den neuen Zähler/die Ableitung des Nenners teilst.) der Bruch durch Polynomdivision (oder geeignetes Ergänzen im Zähler) so umgeformt werden kann, dass für den verbleibenden Restbruch gilt:Zähler = Vielfaches der Nennerableitung

Nun zu der zweiten oben erwähnten Integrationsregel:

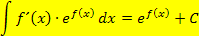
Wie du weißt, darf man bei einem Produkt die Faktoren nicht einzeln integrieren. Sollst du ein Produkt integrieren, bei dem ein Faktor die Form 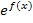besitzt, überprüfst du als allererstes, ob die Ableitung des Exponenten genau dem anderen Faktor des Produkts entspricht. Die Ableitung des Exponenten muss also vor der e-Funktion stehen. Ist dies der Fall, kann die Integrationsregel 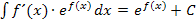verwendet werden. Schauen wir uns das doch gleich an einem konkreten Beispiel an.

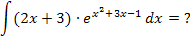
Bei diesem Integral darfst du keinesfalls den ersten Faktor 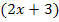einzeln integrieren! Also bitte nicht mit 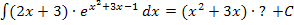beginnen! Das bringt gar nichts. Du musst das gesamte Produkt 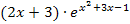betrachten. Der zweite Faktor des Produkts hat die Form 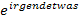, mathematisch gesagt  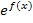. Wenn man die Funktion 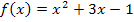, die im Exponenten steht, ableitet, ergibt sich 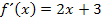. Das ist genau der erste Faktor des Produkts, das wir integrieren sollen.

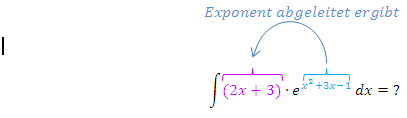
Wir können die Integrationsregel 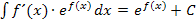anwenden. Das bedeutet, dass du einfach den ersten Faktor des Produkts weglassen musst und schon hast du das Integral berechnet, also eine Stammfunktion ermittelt. So ergibt sich:

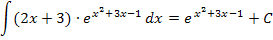
Um dies zu überprüfen, leiten wir die Funktion 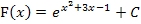ab;es muss sich 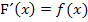ergeben.

---