1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Man muss natürlich derart Ergänzen, dass sich der Nenner beim ersten Teilbruch kürzen lässt. Manchmal verwendet man dabei auch eine Binomische Formel. Wie das konkret funktioniert, kannst du am folgenden Beispiel sehen.
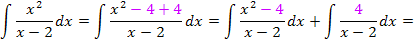
Durch das Ergänzen mit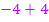 
ergibt sich im Zähler des ersten Teilbruchs die dritte binomische Formel 
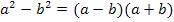. Nach der Anwendung der dritten binomischen Formel lässt sich der Nenner beim ersten Teilbruch komplett wegkürzen.
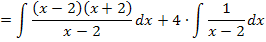
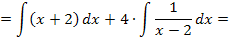
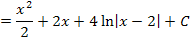
Der Trick mit der Ergänzung des Zählers hilft natürlich nicht immer, sondern nur in ganz bestimmten Sonderfällen. Das Ergänzen des Zählers kommt deshalb nur recht selten vor. Außerdem ist es nicht so leicht zu erkennen, mit was man überhaupt ergänzen muss. Wenn du merkst, dass der Trick mit dem Ergänzen klappt, ist das natürlich super und du darfst das Integral auf diese Art und Weise berechnen. Klappt es nicht oder du kommst selbst zumindest nicht darauf, wie ergänzt werden müsste, hilft meist das zweite Verfahren. Daher solltest dieses zweite Verfahren auf jeden Fall beherrschen.
Unsere zweite Beispielfunktion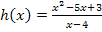 
lässt sich nicht durch Ergänzen des Zählers integrieren. Man könnte im Zähler zwar zu einer zweiten binomischen Formel ergänzen, indem man 
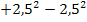hinzufügt;der Nenner ließe sich dann jedoch nicht wegkürzen.
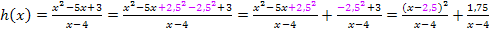
Wie du siehst, hat das nichts gebracht, denn den vorderen Teilbruch kann man nicht integrieren. Wir müssen uns etwas anderes einfallen lassen. Hier hilft uns der zweite Trick.
2. Ausdividieren des Bruchs, z. B. mit Polynomdivision
Man teilt einfach den Zähler des Bruchs soweit möglich durch den Nenner;d.h. man rechnet den Bruch praktisch aus. Bei der Polynomdivision bleibt dabei in der Regel ein Rest. Dieser Rest muss eigentlich auch noch durch den Nenner geteilt werden, weil das aber nicht geht, schreibt man dies einfach als Bruch und addiert ihn zum restlichen Ergebnis der Polynomdivision.
Jetzt machen wir das doch gleich ´mal bei unserer zweiten Beispielfunktion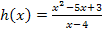 
.
Polynomdivision:
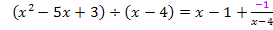
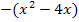
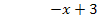
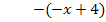
Mit Hilfe der Polynomdivision haben wir die Funktion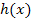 
in eine andere Form umgewandelt.
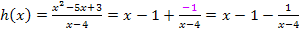
In dieser Form lässt sich die Funktion leicht integrieren. Der vordere Teil kann mit der Regel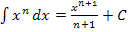 
integriert werden. Der hintere Teil, also der verbleibende Restbruch 
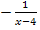, kann hier direkt mit der Regel 
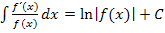integrieren werden, weil der Zähler des Bruchs genau die Ableitung des Nenners ist.
Wenn sich der Restbruch nicht mit der Regel 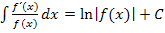integrieren ließe, würde dir diese Methode nichts bringen. Es kann aber sein, dass der Zähler nur ein Vielfaches der Nennerableitung ist;dann musst du einen geeigneten Vorfaktor vor das Integral des Restbruchs schreiben. In diesem Beispiel ist dies nicht nötig.
