1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen

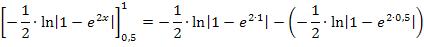
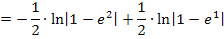
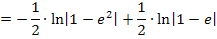
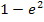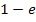Nun stehen wir vor dem Problem mit dem Betrag. Die Ausdrücke und sind beide negativ;das kannst du leicht mit dem Taschenrechner überprüfen. Man darf den Betrag also nicht einfach durch eine Klammer ersetzen. Du solltest den Betrag auflösen;dann lässt es sich nämlich besser weiterrechnen. Der Betrag darf aber erst dann durch eine Klammer ersetzt werden, wenn er sich auf einen positiven Ausdruck bezieht. Wenn man die Reihenfolge bei einer Differenz umdreht, dreht sich bekanntlich das Vorzeichen um;vom Betrag bleibt das Ergebnis aber gleich. Deshalb gilt: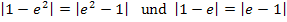

Die Ausdrücke 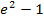und 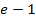sind positiv, nun ist der Betrag unnötig geworden. Es gilt:

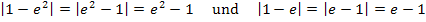
Somit können wir unser Ergebnis auch betragsfrei schreiben:

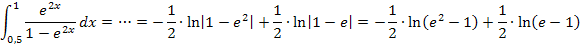
Mit Hilfe der Logarithmus-Rechengesetze kann das gezeigte Ergebnis noch deutlich vereinfacht werden.

Zur Erinnerung:

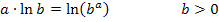
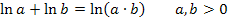
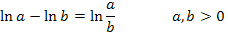
Damit ergibt sich:

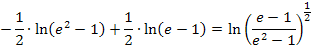
Du hast Schwierigkeiten mit der Anwendung der Logarithmusrechengesetze? Dann gehe zu Logarithmen und Logarithmusrechengesetze;dort findest du ausführlichere Erklärungen und weitere Beispiele dazu.

Statt der Potenz 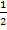schreiben wir die Wurzel, denn bekanntlich gilt: 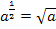. Außerdem verwenden wir im Nenner die dritte binomische Formel 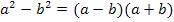. Dann lässt sich nämlich e - 1 kürzen.

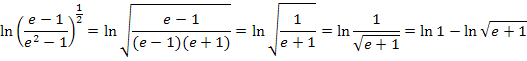
Mit ln1 = 0 ergibt sich: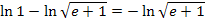

Wer statt der Wurzel die Potenz bevorzugt, kann auch schreiben: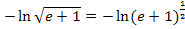

Dies lässt sich auch noch folgendermaßen umformen: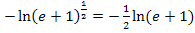

Weiter vereinfachen lässt sich das Ergebnis jetzt nicht mehr. Man könnte es nur noch in den Taschenrechner eingeben und dadurch einen gerundeten Wert ermitteln. Dies sparen wir uns hier.

Das Endergebnis lautet somit:

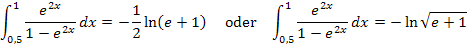
Puh! Das war heftig. Bitte jetzt nicht aufgeben, es wird gleich wieder leichter.

---