1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Die Stammfunktion wird in eckige Klammern geschrieben, wobei an die rechte Klammer oben bzw. unten die jeweilige Integrationsgrenze geschrieben wird. In einem weiteren Schritt werden dann die Grenzen in die Stammfunktion eingesetzt. (Obere Grenze minus untere Grenze) Näheres dazu bei:Das bestimmte und das unbestimmte Integral
Wir müssen also erst einmal eine Stammfunktion zu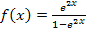 
ermitteln.
Der Nenner ist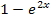 
. Um den Nenner abzuleiten, braucht man unteranderem die Kettenregel. Es handelt sich nämlich bei 
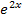um eine verkettete Funktion, wobei y = 2x die innere Funktion darstellt. Die e-Funktion ist die äußere Funktion. Laut Kettenregel wird zuerst die äußere Funktion abgeleitet;die innere bleibt (an Stelle von x) stehen und wird nachdifferenziert. Das bedeutet, dass man noch mit der Ableitung der inneren Funktion multiplizieren muss. Die Ableitung von 
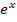ist bekanntlich wieder 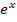. Die Ableitung von 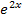ist dann 
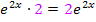. (Die 2 kommt vom Nachdifferenzieren;die innere Funktion y = 2x ergibt abgeleitet schließlich 2.) Die Ableitung des gesamten Nenners, also von 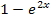, ist entsprechend 
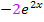. Vorsicht:Das Minus bitte nicht übersehen! Die additive Konstante 1 fällt beim Ableiten weg. Es müsste also 
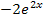im Zähler des Bruchs stehen, damit sich die Integrationsregel 
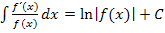anwenden lässt. Der Zähler ist aber 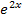;das ist nicht genau die Nennerableitung 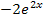, aber ein Vielfaches davon;es fehlt die Zahl – 2. Wir benötigen, wie schon im vorherigen Beispiel, einen entsprechenden Vorfaktor, damit wir die Integrationsregel verwenden können.
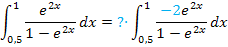
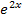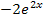Oben wurde bereits erklärt, wie man diesen Faktor findet:Einfach den ursprünglichen Zähler durch den neuen Zähler teilen! In diesem Fall muss also durch geteilt werden. Beim ursprünglichen Zähler denkst du dir eine 1 dazu, also 
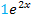durch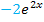 
. Der Term 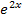kürzt sich letztendlich sowieso weg;du brauchst also nur die Zahlen davor teilen. 1 durch – 2 ergibt 
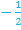;das ist der gesuchte Vorfaktor.
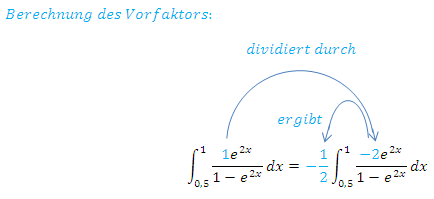
TIPP zur Selbstkontrolle:Der Vorfaktor mit dem neuen Zähler multipliziert muss genau den ursprünglichen Zähler ergeben! Zu deiner eigenen Kontrolle solltest du immer noch einmal schnell überprüfen, ob tatsächlich wieder der ursprüngliche Zähler herauskommt, wenn du den ermittelten Vorfaktor mit dem neuen Zähler multiplizierst. Ansonsten hast du etwas falsch gemacht.
Nun kannst du bestimmt leicht nachvollziehen, wie im nächsten Schritt die Stammfunktion gebildet wird.
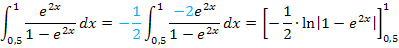
Jetzt müssen die Grenzen eingesetzt und noch alles soweit möglich ausgerechnet werden.
