1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
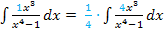
Danach lässt sich die Lösung leicht ermitteln. Es ergibt sich, wie schon oben gezeigt:
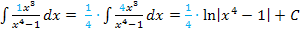
Hast du dir eigentlich die Frage gestellt, warum der Faktor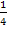 
nicht auch mit der Konstanten C multipliziert wurde? Warum muss man nicht folgendes schreiben:
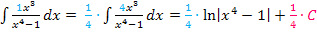
Streng genommen, wird der Faktor 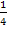komplett aus dem Integral herausgezogen und es ergäbe sich nach dem Ausmultiplizieren tatsächlich 
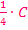und nicht einfach C. Letztendlich ist es jedoch egal, ob man 
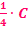oder nur C schreibt. Die Integrationskonstante C ist nämlich sowieso eine unbekannte Zahl. Mit einem kleinen Trick, solltest du das nachvollziehen können. Der Trick besteht darin, einfach als Integrationskonstante vorweg C* zu verwenden und nachher 
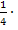C* mit C gleichzusetzen.
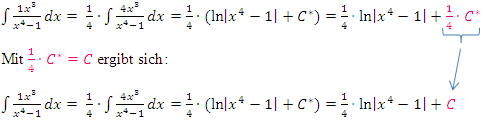
Wenn du selbst rechnest, brauchst du natürlich nicht mit C* zu arbeiten;du darfst direkt + C hinter die Stammfunktion schreiben.
Versuche nun gleich ´mal alleine das oben beschriebene Integrationsverfahren an den folgenden Aufgabenbeispielen anzuwenden!
1. Bsp.:Berechne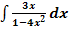 
!
Lösung:
Der Nenner des zu integrierenden Bruchs ist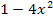 
;abgleitet ergibt das – 8x. Der Zähler des Bruchs, der integriert werden soll, ist 3x;also nicht genau die Nennerableitung, aber ein Vielfaches davon. Die x-Potenz stimmt schon mal. Es kann daher die Integrationsregel 
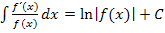angewendet werden, wenn man einen entsprechenden Faktor vor das Integral schreibt.
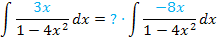
Den gesuchten Faktor findest du, indem du den ursprünglichen Zähler 3x durch den neuen Zähler – 8x teilst. Das x kürzt sich dabei sowieso weg;es muss deshalb eigentlich nur die Zahl 3 durch die Zahl – 8 dividiert werden. Weil sich das nicht weiter ausrechnen lässt, schreiben wir das Ergebnis dieser Division einfach als Bruch. Der benötigte Vorfaktor ist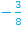 
.
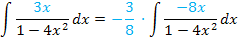
Ab jetzt dürfte die Aufgabe kein Problem mehr darstellen. Jetzt ist der Zähler schließlich genau die Ableitung des Nenners und es kann die Integrationsregel 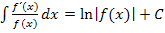angewendet werden.
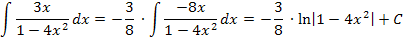
Zur Übung gleich noch ein weiteres, etwas anspruchsvolleres Beispiel. Du solltest es auch wieder zuerst alleine versuchen, bevor du dir die Lösung anschaust.
2. Bsp.:Berechne den Wert des folgenden bestimmten Integrals!
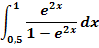
Lösung:
Um ein bestimmtes Integral auszurechnen, muss vorweg eine Stammfunktion ermittelt werden.
