1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Wie würdest du zum Beispiel das Integral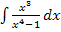 
lösen?
Bitte überlege es dir wirklich alleine, bevor du weiter liest!
Hättest du hier die Zahl 4 vor das Integral geschrieben? Wenn ja, dann hast du es leider genau falsch gemacht. Korrekt ist nämlich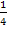 
. Nicht 4, sondern 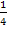muss hier vor das Integral geschrieben werden.
Warum das so ist? Der Nenner ist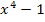 
. Abgeleitet ist dies 
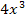. Im Zähler müsste also 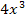stehen, damit sich die Integrationsregel 
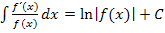anwenden lässt. Es steht aber leider nur 
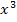im Zähler des zu berechnenden Integrals;es fehlt die Zahl 4 im Zähler. Soweit dürfte die Sache klar sein. Du schreibst nun in den Zähler 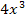und überlegst dir, was zum Ausgleich für die zusätzlich hingeschriebene 4 vor das Integral geschrieben werden muss. Das ist die Zahl 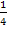und eben nicht 4. Wir dürfen schließlich am gegebenen Integral nicht wirklich etwas verändern;nur Erweitern ist erlaubt. Wenn man im Zähler mit 4 multipliziert, muss man das auch im Nenner tun.
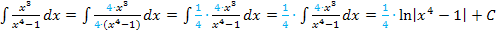
Du siehst, dass im ersten Schritt mit der Zahl 4 erweitert, also im Zähler und Nenner mit 4 multipliziert wurde. An Stelle der Multiplikation des Nenners mit 4 kann der gesamte Bruch auch mit 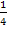multipliziert werden. Das wurde beim zweiten Schritt gemacht. Im vorletzten Schritt wurde die Zahl 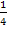vor das Integral gezogen. Das ist erlaubt, da 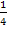eine Konstante ist, d.h. eine Zahl ohne x. (Nur multiplikative Konstanten dürfen vor das Integral geschrieben werden. Ausdrücke, die x enthalten, darfst du niemals vor ein Integral ziehen. Daher muss der Zähler zumindest von der x-Potenz her mit der Ableitung des Nenners übereinstimmen, damit die Integrationsregel 
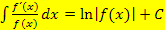angewendet werden kann. Der Zähler muss ein Vielfaches der Nennerableitung sein, sonst kann man die Regel nicht verwenden.)
Der oben gezeigte Weg, wie man den korrekten Vorfaktor findet, ist jedoch viel zu lang. Wir wollen einen schnelleren Weg finden.
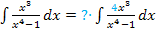
Wie findest du am schnellsten den korrekten Vorfaktor, also diejenige Zahl, die du vor das Integral schreiben musst?
Betrachte zuerst nur den Nenner des Bruchs und bilde die Ableitung. Schreibe statt des ursprünglichen Zählers die Ableitung des Nenners in den Zähler des Bruchs. Den Nenner lässt du unverändert.
Dann teilst du den ursprünglich gegebenen Zähler des zu integrierenden Bruchs durch die Ableitung des Nenners;das ergibt den Vorfaktor, mit dem du multiplizieren musst. Also ursprünglichen Zähler durch neuen Zähler teilen. Das Ergebnis ist die Zahl, die man noch zusätzlich vor das Integral schreiben muss.
