1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Bei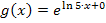 
gilt:a = ln5 und b = 0.)
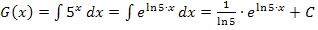
Wir vereinfachen die Stammfunktion noch etwas, indem wir den Ausdruck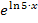 
, wie schon oben bei der Ableitung vorgeführt, umformen: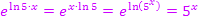 
Somit gilt:
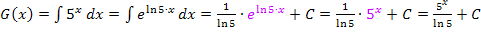
Damit ist die Aufgabe gelöst.
Nun wollen wir uns eine allgemeine Ableitungsregel und eine Integrationsregel für Funktionen der Form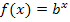 
mit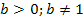 
herleiten. Wir schreiben dafür die Funktion wieder vorab mit der Basis e.
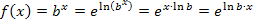
Ableiten mit der Kettenregel ergibt:
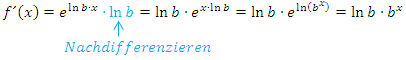
Damit haben wir die folgende Ableitungsregel hergeleitet:
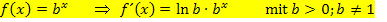
Nun zur Integration von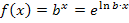 
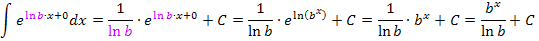
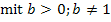
Es wurde dabei die Integrationsformel für lineartransformierte Funktionen verwendet: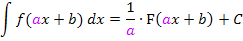 
Zur Erklärung:Das a aus dieser Formel entspricht bei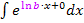 
dem Ausdruck lnb. Das b aus der Integrationsformel für lineartransformierte Funktionen entspricht bei 
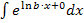der Zahl 0.
Damit haben wir die folgende Integrationsregel hergeleitet:
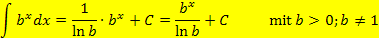
Anmerkung:Auf der Merkhilfe für G8 stehen die soeben hergeleiteten Formeln leider nicht;in der orangen bsv-Formelsammlung für Mathematik, die für FOS/BOS in Bayern zugelassen ist, sind die beiden Formeln erfreulicherweise zu finden.
Wir haben nun die wichtigsten Sonderfälle von Integralen besprochen. Das waren jetzt auch wirklich alle Integrationsregeln, die bayerische Abiturienten für das Abitur benötigen. Wenn du die oben gezeigten Beispiele gründlich durchgearbeitet hast, kennst du alle für´s Abi wichtigen Integrationsformeln. Weitere Integrationsformeln brauchen Abiturienten in Bayern nicht.
Für Schüler eines bayerischen Gymnasiums sind gerade diese Sonderfälle sehr wichtig. Im Abitur werden ähnliche Aufgaben sicher verlangt. Du solltest das Integrieren wirklich sehr gut üben. Du musst dabei leider selbst erkennen, mit welcher Formel du arbeiten musst. Normalerweise sind die Aufgaben bunt gemischt und du musst selbst darauf kommen, nach welcher Methode das vorliegende Integral gelöst werden kann.
Das Problem beim Integrieren komplizierterer Funktionen liegt nämlich vor allem darin, herauszufinden, welche Integrationsregel im speziellen Fall zur Lösung führt. Du musst dir also selbst überlegen, ob ein Integral zum Beispiel auf die Form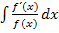 
gebracht werden kann, oder ob ein Integral einer lineartransformierten Funktion vorliegt. Das erkennt man aber meist nur dann, wenn man schon viele Integrale ähnlicher Art berechnet hat. Integrieren ist deutlich anspruchsvoller als Ableiten. Zum Integrieren brauchst du Erfahrung und die Erfahrung bekommst du nur durch viel Übung!
Tipp zum Üben:
