1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen

Tipp zum Integrieren:Formel für linear transformierte Funktionen anwenden!

Hast du es wirklich selbstständig probiert?

Ok;dann der Rest der Lösung.

Hier noch einmal die Funktion: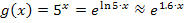

Ableiten mit der Kettenregel ergibt:

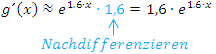
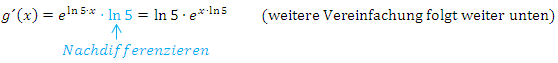
Nicht klar? Also noch einmal ganz langsam:

Die äußere Funktion ist bei 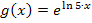die e-Funktion;wir nennen sie u(x). Die innere Funktion nennen wir v(x). Hier gilt: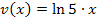

Achtung:Der ln bezieht sich hier nur auf die Zahl 5, nicht aber auf das x dahinter!

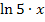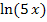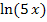ist nicht dasselbe wie ;bei würde sich der ln wegen der Klammer auch auf das x beziehen, aber genau das ist bei 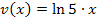eben nicht der Fall!

Laut Kettenregel muss zuerst die äußere Funktion abgeleitet werden. Bei der Ableitung der äußeren Funktion muss aber an Stelle von x die innere Funktion v(x) hingeschrieben werden. Dann muss natürlich noch nachdifferenziert werden, d.h. mit der Ableitung der inneren Funktion multipliziert werden.  Du weißt: 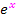abgeleitet ergibt wieder 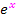. Entsprechend ergibt 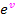nach x abgeleitet 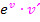. (Das Multiplizieren mit v´ist das Nachdifferenzieren, das nötig ist, weil v hier für die innere Funktion steht. v ist hier eine von x abhängige Funktion.) Nun überlegen wir uns, wie man v´bildet. Was ist die Ableitung von 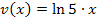? Stelle dir dabei „ 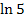“ zur Vereinfachung als „normale Zahl“ vor: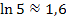

Wie leitest du 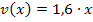ab? Dass 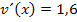gilt, dürfte dir klar sein. Entsprechend gilt: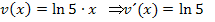

Wir müssen deshalb mit 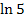nachdifferenzieren.

Nun ist dir hoffentlich klar, warum 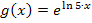abgeleitet 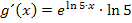ergibt.

Die Ableitung 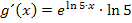lässt sich allerdings noch weiter vereinfachen:

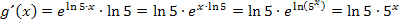
Dir sind die letzten beiden Schritte nicht klar? Ok, dann noch einmal, aber ganz ausführlich:

Lassen wir bei 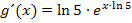mal kurz  ln5 weg und betrachten nur den Ausdruck 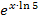. Wie kommt man von 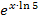zu 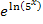und letztendlich auf ?

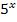Im Exponenten von 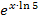, also bei 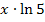lässt sich das folgende Logarithmus-Rechengesetz anwenden: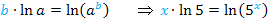

Wir erhalten damit: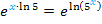

Da die e-Funktion und die ln-Funktion Umkehrfunktionen voneinander sind, heben sie sich gegenseitig auf und es ergibt sich: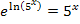

Nun müsste dir die Umformung 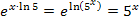einleuchten.

Jetzt zum Integrieren. Wie findet man eine Stammfunktion zu 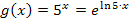? Das geht natürlich genau umgekehrt wie das Ableiten. Beim Ableiten musste mit 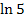multipliziert werden, deshalb muss beim Integrieren durch 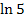dividiert bzw. mit 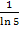multipliziert werden. Dieses Prinzip haben wir ja auch schon bei der Integration linear transformierter Funktionen besprochen. (Die Funktion 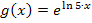ist eine lineartransformierte Funktion, also eine Funktion, bei der für x der Ausdruck 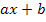eingesetzt ist.

---