1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Der Exponent ist eine konkrete Zahl, nämlich die Zahl 5;er enthält kein x. Man kann „ganz normal“ ableiten bzw. integrieren:
Gegebene Funktion:
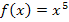
Ableitung:
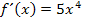
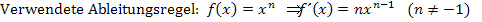
Stammfunktion:
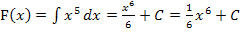
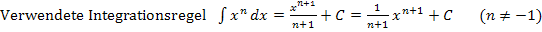
Soweit war das noch ganz einfach, doch bei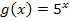 
steht die Variable x im Exponenten und das macht die Sache deutlich komplizierter. x steht hier also oben im Exponenten und nicht wie bei 
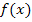unten als Basis! Das macht einen riesigen Unterschied beim Ableiten und Integrieren!
Bevor wir 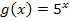ableiten bzw. integrieren können, müssen wir die Funktion mit der Basis e schreiben, weil wir von der bekannten Ableitungsregel 
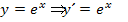bzw. von der Integrationsregel 
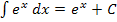ausgehen. Wir bringen die Funktion 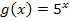also vorweg auf die Form 
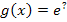. Bloßwie geht das?
Bekanntlich heben sich e-Funktion und ln-Funktion gegenseitig auf, da sie Umkehrfunktionen voneinander sind. Für positive Werte von a gilt daher: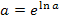 
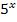ist für beliebige reelle Werte von x immer positiv, da die Basis 5 positiv ist. (Das erkennt man auch am Graph der Funktion 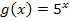:Er verläuft immer oberhalb der x-Achse. Wenn du dir den Graphen nicht vorstellen kannst, siehe Graph der Funktion g!) Weil 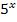immer positive Werte ergibt, dürfen wir die folgende Umformung durchführen:
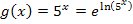
Als nächstes wenden wir im Exponenten das Logarithmusrechengesetz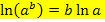 
an.
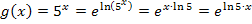
Achtung:Der ln im Exponenten von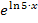 
bezieht sich nur auf die Zahl 5, nicht aber auf das x dahinter.
Stelle dir jetzt vorübergehend „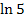 
“ zur Vereinfachung als „normale Zahl“ vor: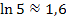 
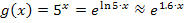
Hinweis:Schüler eines bayerischen Gymnasiums G8 kommen um die soeben gezeigte Umformung nicht herum, da zwar die Ableitung bzw. Stammfunktion der e-Funktion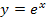 
auf der Merkhilfe steht, jedoch nicht die Ableitung bzw. Stammfunktion von Funktionen der Form 
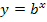. Gymnasiasten (G8) müssen zwangsläufig von der einzig hilfreichen, bekannten Ableitungsregel 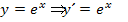bzw. von der Integrationsregel 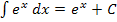ausgehen. (Schüler einer FOS/BOS müssen diesen umständlichen Weg nicht unbedingt verwenden. Sie können stattdessen auch einfach die Ableitungs- bzw. Integrationsregel für Funktionen der Form 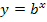verwenden;in der orangen bsv-Formelsammlung sind sie zu finden. Wir werden sie am Ende dieses Beispiels gleich noch zeigen.)
Ab jetzt müsstest du alleine weiterrechnen können. Versuche zuerst selbständig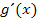 
und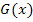 
zu finden, bevor du den Rest der Lösung liest!
Tipp zum Ableiten:Kettenregel verwenden!
