1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Die Zahl 7 bleibt beim Integrieren stehen. Es handelt sich bei der 7, wie schon vorher bei der Zahl 6 im ersten Integral, um eine multiplikative Konstante, also um eine Zahl, die multipliziert wird. Solche Zahlen werden beim Integrieren grundsätzlich abgeschrieben. (Man darf sie gemäßdem Gesetz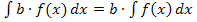 
vor das Integral ziehen. Es gilt somit: 
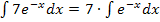Daher kann man in diesem Fall die Zahl 7 beim Integrieren einfach abschreiben.)
Dir ist nicht klar, warum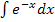 
mit der Formel 
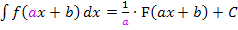gelöst werden kann?
Dann denke dir statt 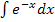einfach 
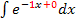. Daran lässt sich leichter erkennen, dass die Grundfunktion 
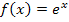und die lineare Funktion 
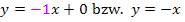ist. Der Koeffizient a ist dabei – 1. Vorsicht:Bei der Berechnung von 
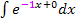den Faktor 
nicht vergessen! Du musst hier also 
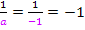dazu schreiben, wenn du integrierst.
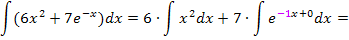
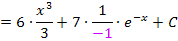
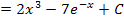
Zu 5j.)
Hier noch einmal die Angabe: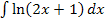 
Offensichtlich handelt es sich dabei um das Integral einer lineartransformierten Funktion. In die Grundfunktion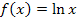 
ist die lineare Funktion 
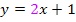eingesetzt. Der Koeffizient a ist 2. Laut der Formel 
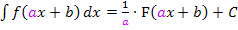müssen wir die Integration mit 
, also mit 
beginnen. Nun brauchen wir die Stammfunktion F(x) der Grundfunktion 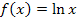. In deiner Formelsammlung bzw. auf deiner Merkhilfe findest du die Formel 
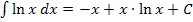. Für jedes auftretende x müssen wir allerdings den Ausdruck 
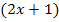schreiben.
Vorsicht:Der Faktor 
muss sich auf den kompletten folgenden Ausdruck beziehen, daher benötigt man eine Klammer um den gesamten folgenden Ausdruck. (Rote eckige Klammer)
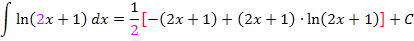
Man könnte noch den Faktor in die eckige Klammer hineinmultiplizieren.
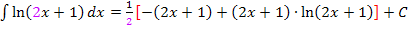
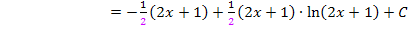
Das macht das Ganze aber auch nicht einfacher. Daher kannst du dir den letzten Schritt auch sparen.
Nun haben wir wirklich viele Aufgaben mit Integralen lineartransformierter Funktionen gerechnet. Das Prinzip müsstest du inzwischen verstanden haben.
Aus meiner langjährigen Nachhilfetätigkeit weißich allerdings, dass viele Schüler zu Beginn Schwierigkeiten haben beim Integrieren, beispielsweise die Unterscheidung der komplett unterschiedlichen Methoden der Integration von Funktionen der Form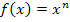 
und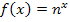 
. Daher noch eine abschließende Beispielaufgabe zu diesem speziellen Problem.
6. Bsp.:Wir betrachten die Funktionen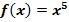 
und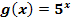 
. Bilde zu beiden Funktionen jeweils die Ableitung und die Stammfunktion.
Hinweis:Schreibe die Funktion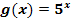 
vorher mit der Basis e!
Lösung:
Die Funktion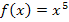 
ist einfach abzuleiten und zu integrieren, da hier die Variable x die Basis ist;x steht bei 
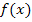unten und nicht oben im Exponenten.
