1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
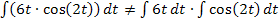
Nun aber wieder zurück zu unserer Aufgabe. Wir müssen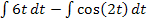 
berechnen. Die Variable heißt in diesem Fall nicht x, sondern t. Das stellt aber kein besonderes Problem dar. t entspricht praktisch x. Du verfährst mit dem t genauso wie sonst mit x.
Das erste Integral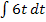 
ist ganz einfach zu lösen. Die Zahl 6 ist eine multiplikative Konstante, d.h. eine Zahl, die multipliziert wird. Sie darf beim Integrieren einfach abgeschrieben werden;es muss dann nur noch das t integriert werden. Statt t kannst du dir 
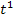denken und die normale Integrationsregel 
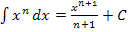verwenden. Das t entspricht dabei dem x in der Formel. Wir integrieren schließlich nach dt.
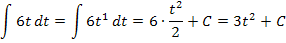
Jetzt zum zweiten Integral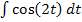 
. Wie kann man das berechnen?
Hast du es erkannt? Es ist das Integral einer linear transformierten Funktion. Wenn dir das nicht klar ist, denkst du dir innerhalb der Klammer eine Null addiert:
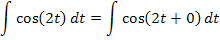
Nun müsste dir klar sein, dass es sich um ein Integral der Form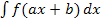 
handelt. (Die Variable ist allerdings nicht x, sondern t.) Wir können die Formel für linear transformierte Funktionen anwenden:
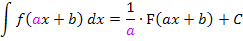
Die Grundfunktion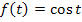 
ist mit der linearen Funktion 
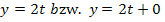verkettet. Mit der Stammfunktion 
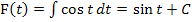ergibt sich:
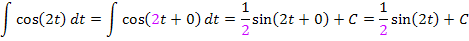
Insgesamt lautet die Lösung des gesuchten Integrals:
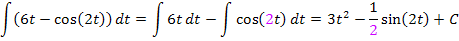
Hinweis:Der Faktor 
darf nicht ganz nach vorne geschrieben werden, denn er bezieht sich wirklich nur auf den hinteren Teil, also nur auf den Ausdruck 
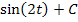, nicht aber auf 
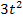. Das war auch der Grund, warum wir das Integral in zwei Einzelintegrale aufgeteilt haben. So ist es bestimmt leichter für dich.
Zu 5h.)
Hier noch einmal die Angabe: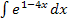 
Es handelt sich um das Integral einer lineartransformierten Funktion. Die Grundfunktion ist hier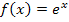 
. Die lineare Funktion ist 
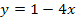. Wenn du dabei die Reihenfolge der Faktoren umdrehst, erhältst du 
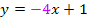. So erkennst du besser, dass der Koeffizient a die Zahl – 4 ist. Die Integration muss laut der Formel 
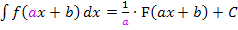mit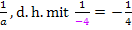 
begonnen werden.
Mit der Stammfunktion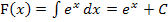 
der Grundfunktion 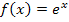ergibt sich:
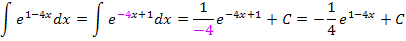
Zu 5i.)
Hier noch einmal das zu lösende Integral: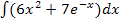 
Wie schon in Teilaufgabe 5g.) erläutert, teilen wir das Integral in zwei einzelne Integrale auf.
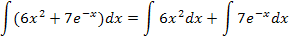
Das vordere Integral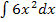 
stellt kein Problem dar, es kann mit der Formel 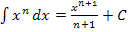gelöst werden. Die Zahl 6 kann vor das Integral gezogen, d.h. bei der Integration letztendlich einfach abgeschrieben werden.
Das zweite Integral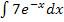 
kann mit der Formel für linear transformierte Funktionen gelöst werden.
