1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Die Grundfunktion ist hier allerdings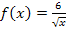 
und die lineare Funktion ist 
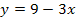. Du solltest bei der linearen Funktion die Reihenfolge der einzelnen Glieder vertauschen, also statt 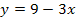besser 
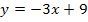schreiben. Dann kannst du leichter erkennen, dass a hier – 3 ist. Los geht die Integration daher mit 
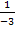bzw. mit 
.
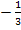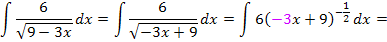
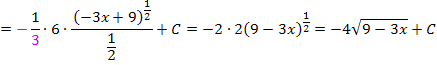
Nicht klar? Ok, dann alles noch einmal ganz langsam Schritt für Schritt.
Wir bilden erst einmal die Stammfunktion F(x) der Grundfunktion 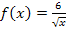. Wir müssen also 
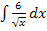berechnen.
Dafür formen wir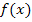 
mit den folgenden Potenzgesetzen um: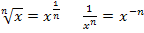 
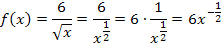
Die Integration erfolgt nun nach der Regel: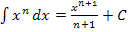 
Die Zahl 6 wird einfach abgeschrieben, da es sich um eine multiplikative Konstante handelt, also um eine Zahl, mit der multipliziert wird. Solche Zahlen bleiben beim Integrieren (genauso wie beim Ableiten) einfach stehen.
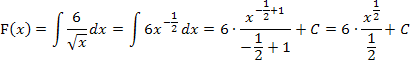
Man dividiert bekanntlich durch einen Bruch, indem man mit dem Kehrwert multipliziert. Daher teilt man durch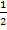 
, indem man mit 
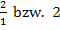multipliziert. Außerdem schreiben wir statt 
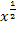besser 
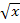. (Die Schreibweise mit den Potenzen wurde zwischenzeitlich nur deshalb verwendet, weil man damit leichter integrieren konnte. Im Endergebnis sollen aber eigentlich keine negativen Zahlen oder Brüche im Exponenten vorkommen.)
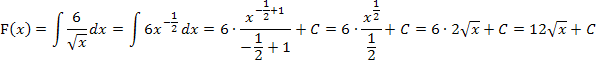
Um die Lösung von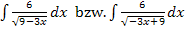 
zu erhalten, muss nun bei F(x) das x durch den Ausdruck 
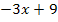ersetzt werden und außerdem mit dem Faktor 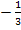multipliziert werden.
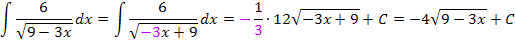
Ob du lieber den schnellen Weg verwendest oder den als zweiten gezeigten, ausführlichen Rechenweg, bleibt dir selbst überlassen.
Zu 5f.)
Hier noch einmal die Angabe: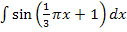 
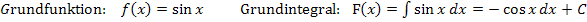
Lineare Funktion: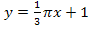 
Verwendete Integrationsformel: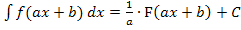 
Der Koeffizient a ist hierbei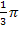 
.
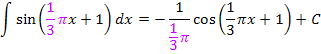
Hinweis:
Das Minuszeichen ganz am Anfang kommt von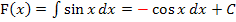 
. Das Minus wurde einfach vor den Faktor 
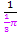gezogen.
Man teilt bekanntlich durch einen Bruch, indem man mit dem Kehrwert multipliziert. Statt „durch 
“ kann man „mal 
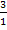“ , also „mal 3“ rechnen. Deshalb schreibt man an Stelle von im Nenner die Zahl 3 in den Zähler.
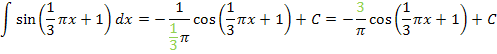
Zu 5g.)
Hier noch einmal das zu berechnende Integral: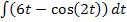 
Am einfachsten ist es, wenn man dieses Integral in zwei einzelne Integrale aufteilt.
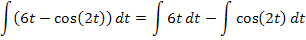
Anmerkung:
Bei Summen oder Differenzen, also bei Plus oder Minus ist es erlaubt, ein Integral aufzuteilen. Es gilt nämlich:
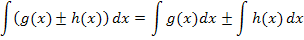
Bei einem Produkt oder Quotienten zweier Funktionen, d.h. bei mal oder geteilt wäre es nicht erlaubt gewesen.
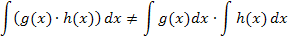
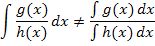
Hätte das Integral beispielsweise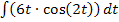 
gelautet, hätte man nicht in zwei Einzelintegrale zerlegen dürfen!
