1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
)
Hier noch einmal die Angabe: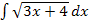 
Es handelt sich natürlich wieder um das Integral einer linear transformierten Funktion. In die Grundfunktion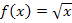 
ist die lineare Funktion 
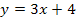eingesetzt. Der Koeffizient a ist hier offensichtlich die Zahl 3. (Es steht schließlich 3 vor dem x.) Wir beginnen bei der Integration linear transformierter Funktionen immer mit 
, hier also mit 
.
Dann ermitteln wir die Stammfunktion F(x) der Grundfunktion 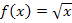. Vorweg formen wir die Funktion 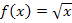in eine Potenzfunktion (d.h. eine Funktion der Form 
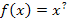) um, damit wir dann die Integrationsregel 
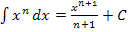benutzen können. Dabei verwenden wir das Potenzgesetz 
.
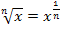Man teilt durch einen Bruch, indem man mit dem Kehrwert multipliziert. Daher schreiben wir statt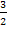 
im Nenner 
vor den Bruch. Den Ausdruck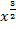 
formen wir auch noch um;ein Bruch im Exponenten ist nämlich nicht schön. Wir schreiben das besser als Wurzel. Wir benutzen dabei das Potenzgesetz 
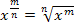. (Zur Erinnerung:Die zweite Wurzel 
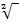ist die „normale“ Wurzel 
.)
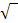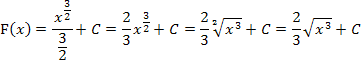
In dieser Form könnten wir mit F(x) bereits weiterrechnen. Eleganter ist es jedoch, wenn man noch teilweise radiziert, d.h. wenn man noch teilweise die Wurzel zieht. Statt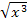 
kann man auch 
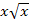schreiben. Wie man darauf kommt?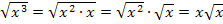 
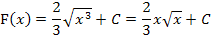
Jetzt kennen wir die Stammfunktion F(x) der Grundfunktion .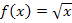
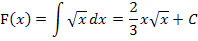
Wenn man das gesuchte Integral 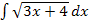berechnen will, muss man jedoch jedes in F(x) vorkommende x noch durch den Ausdruck 
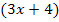ersetzen. Außerdem dürfen wir den Faktor nicht vergessen, den wir uns vorher schon überlegt haben. (Beim Ableiten von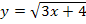 
müsste man schließlich mit 3 nachdifferenzieren, d.h. multiplizieren. Deshalb muss bei der Integration entsprechend umgekehrt durch 3 dividiert bzw. mit multipliziert werden.)
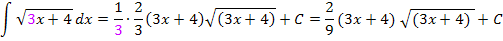
Zu 5d.)
Hier noch einmal das zu lösende Integral: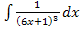 
In die Grundfunktion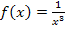 
ist die lineare Funktion 
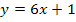eingesetzt. Es handelt sich also um das Integral einer linear transformierten Funktion.
Der Koeffizient a ist offensichtlich die Zahl 6. Wir dürfen nachher nicht vergessen mit , hier also mit 
zu multiplizieren.
Vorweg berechnen wir die Stammfunktion F(x) der Grundfunktion 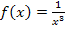, d.h. das Grundintegral 
.
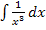Dabei benötigtes Potenzgesetz: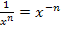 
Die Integration erfolgt nach der Regel: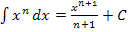
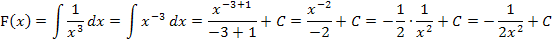
Wir ersetzen nun x durch den Ausdruck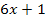 
und multiplizieren außerdem mit dem Faktor 
.
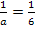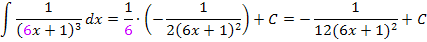
Wenn du auf die Nebenrechnung für das Grundintegral verzichten möchtest, kannst du auch folgendermaßen rechnen:
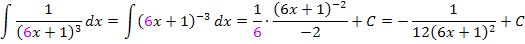
Zu 5e.)
Berechnet werden soll: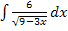 
Die Berechnung dieses Integrals ist ganz ähnlich wie bei den vorher gezeigten Teilaufgaben.
