1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Besonders wichtig ist bei der Integration von linear transformierten Funktionen das a, also die Zahl, die vor dem x steht. Bei der Stammfunktion muss anfangs nämlich immer mit 
multipliziert werden. Bei der Berechnung von Integralen der Form 
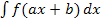muss also mit 
begonnen werden. wird dann mit der Stammfunktion F der Grundfunktion f multipliziert, bei der jedoch jedes vorkommende x durch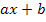 
ersetzt ist. Das ist mit der Formel 
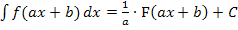gemeint. Wie dies genau funktioniert, schauen wir uns besser an einem konkreten Beispiel an.
Wir bleiben bei dem Beispiel der lineartransformierten Funktion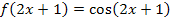 
;nun soll sie integriert werden, d.h. wir müssen das Integral 
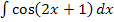berechnen. Bloß, wie geht das?
Bevor wir integrieren, überlegen wir uns, wie man die Funktion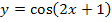 
ableiten würde. Man bräuchte bei dieser Funktion zum Ableiten die Kettenregel, welche besagt, dass zuerst die äußere Funktion (hier die Kosinus-Funktion) abgeleitet werden muss, dabei bleibt die innere Funktion an Stelle von x stehen, sie muss aber noch nachdifferenziert werden. Nachdifferenzieren heißt bekanntlich, mit der Ableitung der inneren Funktion (hier der linearen Funktion 
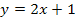) multiplizieren. Die Ableitung von 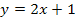ist die Zahl 2;es müsste daher beim Ableiten von 
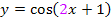mit 2 nachdifferenziert, d.h. mit 2 multipliziert werden. Die Ableitung von 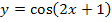wäre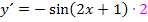 
oder wenn man die 2 nach vorne zieht 
.
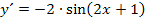Beim Integrieren von 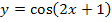muss man es entsprechend genau umgekehrt machen wie beim Ableiten. Weil beim Ableiten mit 2 nachdifferenziert/multipliziert werden muss, muss beim Integrieren durch 2 dividiert bzw. mit 
multipliziert werden. Nur die äußere Funktion, also die Grundfunktion (hier: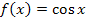 
) wird dann integriert, wobei die innere Funktion (hier: 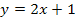) an Stelle von x hingeschrieben wird. Den Ausdruck 
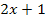darfst du also nicht integrieren;er wird bei F wirklich nur statt x hingeschrieben.
Hinweis:Stammfunktion von 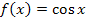ist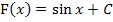 
.
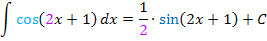
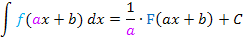
Fassen wir die Vorgehensweise beim Integrieren an diesem konkreten Beispiel noch einmal zusammen.
Berechnung von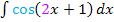 
:
- Schreibe „1 durch diejenige Zahl, die vor dem x steht“, d.h. schreibe als erstes
hin. - Nimm die Grundfunktion
und bilde eine Stammfunktion F, wobei du für jedes x den Ausdruck 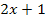einsetzt. (Stammfunktion von ist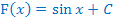 
.) Du schreibst also 
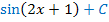hinter den vorher schon hingeschriebenen Faktor . Fertig!
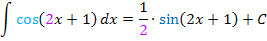
Nun übertagen wir dies auf den allgemeinen Fall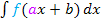 
.
Integration linear transformierter Funktionen / Berechnung von  :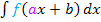
In anderen Worten:Bei der Berechnung des Integrals einer linear transformierten Funktion also von Integralen der Form Genau das besagt die Formel |
hin.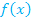
und bilde eine Stammfunktion F, wobei du statt x den Ausdruck 
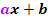schreibst. Dies multiplizierst du mit dem Faktor 
, den du vorher bereits hingeschrieben hast. Fertig!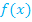
;dann ersetzt du jedes auftretende x durch den Ausdruck 
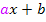. Vor das Ganze setzt du den Faktor 
.
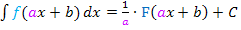.Nun wenden wir dieses Verfahren gleich ´mal bei einigen Beispielaufgaben an.
