1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Dass der Faktor, den wir vor das Integral gezogen haben, korrekt ist, kannst du leicht kontrollieren, indem du einfach 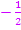 mit
mit 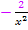 multiplizierst;es muss wieder
multiplizierst;es muss wieder 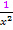 herauskommen. Das tut es natürlich auch. Der Faktor ist korrekt.
herauskommen. Das tut es natürlich auch. Der Faktor ist korrekt.
Nun ist der erste Faktor des Produkts die Ableitung des Exponenten und wir können die Regel 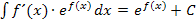 anwenden, um das Integral zu lösen. So ergibt sich der komplette Lösungsweg.
anwenden, um das Integral zu lösen. So ergibt sich der komplette Lösungsweg.
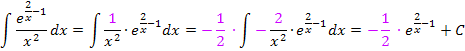
Nun zur letzten der oben aufgeführten Integrationsregeln: 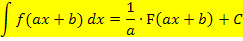
Eine Funktion der Form 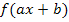 nennt man linear transformierte Funktion. So eine Funktion entsteht durch Verkettung einer Funktion
nennt man linear transformierte Funktion. So eine Funktion entsteht durch Verkettung einer Funktion 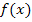 mit einer linearen Funktion, d.h. einer Geraden. (Siehe auch:Verketten/Verkettete Funktion) Die Gerade stellt dabei die innere Funktion dar. Die äußere Funktion
mit einer linearen Funktion, d.h. einer Geraden. (Siehe auch:Verketten/Verkettete Funktion) Die Gerade stellt dabei die innere Funktion dar. Die äußere Funktion 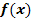 , also diejenige Funktion in die die Innere eingesetzt wird, wird bei der linearen Transformation als Grundfunktion bezeichnet.
, also diejenige Funktion in die die Innere eingesetzt wird, wird bei der linearen Transformation als Grundfunktion bezeichnet.
Du kennst sicher die allgemeine Geradengleichung  , wobei m für die Steigung der Geraden und t für den y-Achsenabschnitt steht. Statt m und t schreiben wir jetzt a und b. (Wir machen dies, weil auf der Merkhilfe für G8 in diesem Zusammenhang ebenfalls die Bezeichnungen a und b verwendet werden.) Setzt man eine Gerade
, wobei m für die Steigung der Geraden und t für den y-Achsenabschnitt steht. Statt m und t schreiben wir jetzt a und b. (Wir machen dies, weil auf der Merkhilfe für G8 in diesem Zusammenhang ebenfalls die Bezeichnungen a und b verwendet werden.) Setzt man eine Gerade 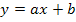 in eine Funktion
in eine Funktion 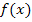 ein, erhält man die linear transformierte Funktion
ein, erhält man die linear transformierte Funktion 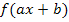 . Mathematisch gesagt, es wird die Funktion
. Mathematisch gesagt, es wird die Funktion 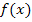 mit der Gerade
mit der Gerade 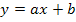 verkettet. Dabei stellt die Gerade die innere Funktion dar.
verkettet. Dabei stellt die Gerade die innere Funktion dar.
Beispiel:Nehmen wir die Grundfunktion 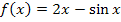 und die Gerade
und die Gerade 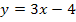 .
.
Wir setzen die Gerade 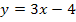 in
in 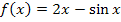 ein:
ein:
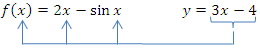
So ergibt sich die lineartransformierte Funktion 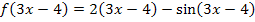 .
.
In jedes x, welches bei 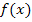 vorkommt, wurde also
vorkommt, wurde also 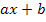 (hier:
(hier: 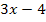 ) eingesetzt.
) eingesetzt.
Allgemein schreibt man:
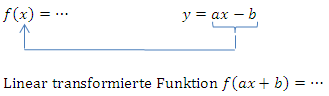
Die Verkettung musst du normalerweise nicht selbst durchführen;die Funktion 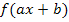 ist bereits gegeben, du sollst sie dann integrieren. Dazu musst du jedoch selbst erkennen, dass es sich bei einer Funktion der Form
ist bereits gegeben, du sollst sie dann integrieren. Dazu musst du jedoch selbst erkennen, dass es sich bei einer Funktion der Form 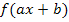 um eine linear transformierte Funktion handelt. Dann kannst du nämlich die oben aufgeführte Formel anwenden, um die Funktion zu integrieren. Wie das geht, wird gleich noch ausführlich erklärt.
um eine linear transformierte Funktion handelt. Dann kannst du nämlich die oben aufgeführte Formel anwenden, um die Funktion zu integrieren. Wie das geht, wird gleich noch ausführlich erklärt.
Sollst du beispielsweise das Integral 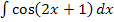 berechnen, musst du erkennen, dass es sich bei der Funktion
berechnen, musst du erkennen, dass es sich bei der Funktion 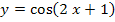 um eine linear transformierte Funktion handelt. In die Grundfunktion
um eine linear transformierte Funktion handelt. In die Grundfunktion 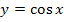 ist die lineare Funktion
ist die lineare Funktion 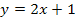 eingesetzt.
eingesetzt.

So ergibt sich die lineartransformierte Funktion 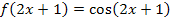 .
.
In jedes x, welches bei 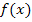 vorkommt, wurde also
vorkommt, wurde also 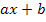 (hier:
(hier: 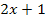 ) eingesetzt.
) eingesetzt.
Die lineare Funktion 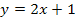 hat die Steigung a = 2 (sonst:m genannt) und den y-Achsenabschnitt b = 1 (sonst:t genannt).
hat die Steigung a = 2 (sonst:m genannt) und den y-Achsenabschnitt b = 1 (sonst:t genannt).

