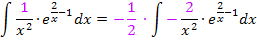1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen

Dir ist nicht klar, wie man auf die Ableitung des Exponenten gekommen ist? Ok, dann noch einmal ganz langsam.

Nebenrechnung:

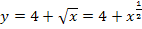
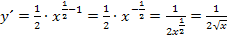
Wie berechnen wir nun das Integral ?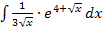

Der Exponent ist 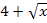. Die Ableitung des Exponenten ist 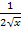. Der erste Faktor des Produkts, das integriert werden soll, ist aber 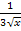. Das ist zwar ein Vielfaches der Ableitung des Exponenten, aber nicht exakt die Ableitung davon. Wir brauchen daher einen Korrekturfaktor, d.h. eine Zahl, die man zum Ausgleich vor das Integral schreibt, damit der erste Faktor des Produkts genau der Ableitung des Exponenten entspricht.

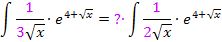
Doch welchen Faktor müssen wir hier vor das Integral setzen? Am leichtesten ist das zu ermitteln, wenn man den ersten Faktor des ursprünglichen Integrals 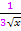durch die Ableitung des Exponenten 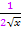dividiert. Eigentlich reicht es völlig aus, wenn man nur durch teilt und dabei 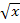völlig ignoriert; 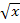kürzt sich nämlich sowieso heraus.

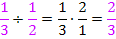
Das kannst du natürlich auch mit dem Taschenrechner ausrechnen. Auf jeden Fall weißman jetzt, dass der Faktor zum Ausgleich vor das Integral geschrieben werden muss.

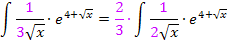
Nun ist der erste Faktor des Produkts die Ableitung des Exponenten und wir können die Regel 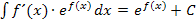anwenden, um das Integral zu lösen. So ergibt sich der komplette Lösungsweg.

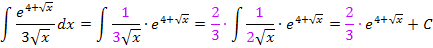
Zu 4e.)

Hier noch einmal die Angabe: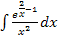

Dieses Integral kann nach dem gleichen Prinzip gelöst werden, wie das vorherige aus Teilaufgabe 4d. Wir schreiben wieder den Bruch als Produkt. Überlegen uns dann die Ableitung des Exponenten und schauen, ob er mit dem einen Faktor des Produkts übereinstimmt. Es handelt sich bei der Ableitung des Exponenten nicht exakt um den ersten Faktor des zu integrierenden Produkts, sondern nur um ein Vielfaches davon. Daher benötigen wir noch den Ausgleichsfaktor, den wir vor das Integral ziehen müssen, damit der erste Faktor des Produkts genau zur Ableitung des Exponenten wird. Versuche das nun wirklich erst alleine zu rechnen! Dann kannst du dein Ergebnis mit der folgenden Lösung vergleichen.

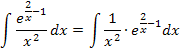
Nebenrechnung:

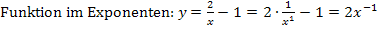
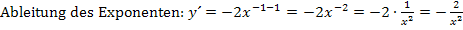
Der erste Faktor des zu integrierenden Produkts ist allerdings nicht 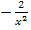, sondern 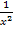. Der erste Faktor soll aber gleich der Ableitung des Exponenten sein. Er müsste also 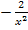sein. Wir brauchen einen Korrekturfaktor, den wir vor das Integral schreiben.

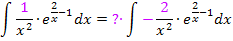
Diesen Faktor finden wir, indem wir 1 durch – 2 teilen;das ergibt natürlich .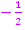

---