1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Letztendlich ist es jedoch egal, ob man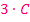 
oder nur C schreibt. Die Integrationskonstante C ist nämlich sowieso eine unbekannte Zahl.
Mit einem kleinen Trick, solltest du das nachvollziehen können. Der Trick besteht darin, einfach als Integrationskonstante vorweg C* zu verwenden und nachher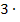 
C* mit C gleichzusetzen. (Diesen Trick haben wir weiter oben schon einmal bei der Integrationsregel 
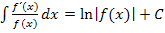besprochen.)
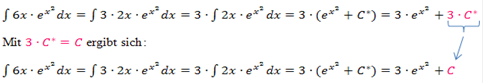
Wenn du selbst rechnest, brauchst du natürlich nicht mit C* zu arbeiten;du darfst direkt + C hinter die Stammfunktion schreiben.
Zu 4b.)
Hier noch einmal die Angabe: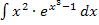 
Auch bei dieser Aufgabe stimmt die Ableitung des Exponenten nicht genau mit dem ersten Faktor des Produkts überein. Der Exponent ist hier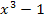 
. Die Ableitung des Exponenten ist bekanntlich 
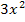. Der erste Faktor des zu integrierenden Produkts ist aber nicht 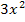, sondern nur 
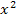. Es fehlt praktisch die Zahl 3. Dieses Problem lösen wir folgendermaßen:
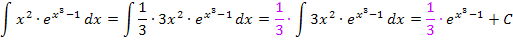
Den ersten Zwischenschritt kann man natürlich auch überspringen. Um den benötigten Vorfaktor zu finden, kannst du auch einfach den ursprünglichen ersten Faktor des Produkts durch die Ableitung des Exponenten teilen. Das Ergebnis ist diejenige Zahl, die du vor das Integral schreiben musst, damit sich die Regel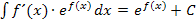 
anwenden lässt. In diesem Beispiel musst du also 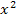(den ursprünglichen ersten Faktor des Produkts) durch 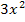(die Ableitung des Exponenten) teilen. 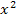bzw. 
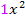dividiert durch 
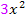ergibt die Zahl 
, welche vor das Integral geschrieben werden muss, damit man die Integrationsregel 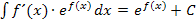anwenden kann.
Diese Vorgehensweise ähnelt sehr stark dem Prinzip, das wir schon bei der Regel 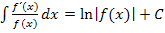kennengelernt haben. (Vergleiche 1. Bsp.)
Zu 4c.)
Hier noch einmal das Integral, das berechnet werden soll: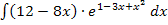 
Wir betrachten wieder zuerst den Exponenten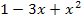 
. Seine Ableitung ist 
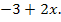Der erste Faktor des zu integrierenden Produkts ist leider nicht 
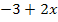, sondern 
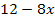. Du kannst nun entweder 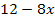durch 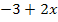dividieren oder einfacher aus 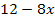die Zahl – 4 ausklammern und dann vor das Integral ziehen.
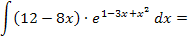
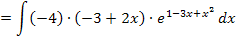
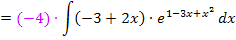
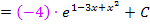
Zu 4d.)
Hier noch einmal die Angabe: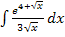 
Um diese Aufgabe zu lösen, müssen wir den Bruch vorweg als Produkt schreiben.
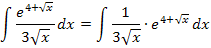
Nun ist besser zu erkennen, dass uns hier die Integrationsregel 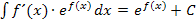weiter hilft, auch wenn sie nicht direkt angewendet werden kann. Die Ableitung des Exponenten 
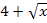ist nämlich nicht 
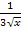, sondern 
.
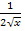