1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen

So ergibt sich der neue Exponent.)

Nebenrechnung:

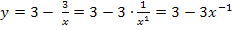
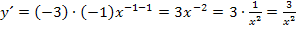
Nun siehst du, dass die Ableitung des Exponenten dem ersten Faktor des zu integrierenden Produkts entspricht. Es lässt sich die Regel 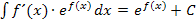anwenden. Damit erhalten wir die Lösung:

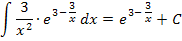
Zu 3d.)

Hier noch einmal das Integral, das berechnet werden soll: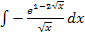

Wir gehen so ähnlich vor, wie schon in Teilaufgabe 3c. erläutert. D.h. wir formen den Bruch in ein Produkt um und schauen dann, ob die Ableitung des Exponenten dem ersten Faktor des Produkts entspricht. Um die Ableitung des Exponenten zu bilden, wird hier vorweg allerdings das Potenzgesetz 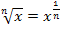angewendet. Es gilt: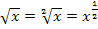

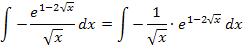
Nebenrechnung:

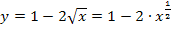
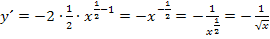
Die Ableitung des Exponenten entspricht also dem ersten Faktor des zu integrierenden Produkts. Es lässt sich die Regel 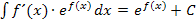anwenden. Damit erhalten wir die Lösung:

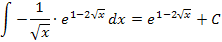
Nun denkst du dir vielleicht:Warum soll ich denn überhaupt die Ableitung des Exponenten bilden, wenn diese Ableitung sowieso immer den ersten Faktor des Produkts bildet, welches integriert werden soll? Da kann ich doch gleich die Integrationsregel 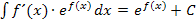anwenden.

Es ist natürlich nicht immer so, dass die Ableitung genau dem ersten Faktor des Produkts entspricht. Das war zwar im 3. Bsp. der Fall, aber im nächsten Beispiel wird dies nicht mehr so einfach sein. Außerdem gibt es andere Integrale, die sich so überhaupt nicht lösen lassen. Du musst schon selbst überprüfen, ob der eine Faktor des zu integrierenden Produkts der Ableitung des Exponenten der e-Funktion entspricht.

4. Bsp.:Berechne die folgenden unbestimmten Integrale!

a.)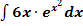

b.)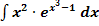

c.)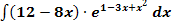

d.)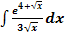

e.)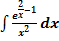

Lösung:

Zu 4a.)

Um das Integral 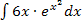zu berechnen, betrachten wir wieder zuerst den Exponenten und überlegen uns, was seine Ableitung ist. 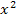ergibt abgeleitet bekanntlich 2x und nicht 6x. In diesem Fall stimmt der erste Faktor des Produkts also nicht exakt mit der Ableitung des Exponenten überein;es handelt sich aber zumindest um ein Vielfaches davon. An Stelle von 6x schreiben wir nun einfach 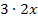und ziehen dann den Faktor 3 vor das Integral, erst dann lässt sich die Regel 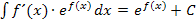anwenden.

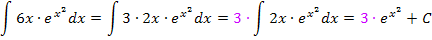
Hast du dir eigentlich die Frage gestellt, warum der Faktor 3 nicht auch bei der Konstanten C steht? Warum muss man nicht folgendes schreiben:

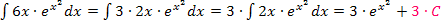
Streng genommen, wird der Faktor 3 komplett aus dem Integral herausgezogen und es ergäbe sich, wenn man die 3 wieder in die Klammer hineinmultipliziert, tatsächlich 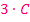und nicht einfach C.

---