1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen

Dann wenden wir diese Regel bei den folgenden Beispielen doch gleich ´mal an! Am besten ist es natürlich, du probierst es erst einmal alleine, bevor du dir die Lösungen ansiehst.

Im 3. Bsp. kann bei allen Teilaufgaben die Regel direkt angewendet werden, ohne dass mit einem Ausgleichsfaktor gearbeitet werden muss. In anderen Worten:Die Ableitung des Exponenten entspricht genau dem ersten Faktor des Produkts, das integriert werden soll. Man muss keine Zahl vor das Integral ziehen. Allerdings musst du die zu integrierende Funktion manchmal vorweg noch anders hinschreiben, damit du das überhaupt erkennen kannst. Das ist das Problem bei den Teilaufgaben 3b. bis 3d.

Im 4. Bsp. wird gezeigt, wie sich die Regel 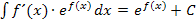anwenden lässt, wenn der erste Faktor  nicht genau der Ableitung des Exponenten entspricht, sondern nur einem Vielfachen davon. Los geht´s!

3. Bsp.:Berechne die folgenden Integrale!

a.)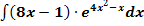

b.)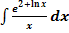

c.)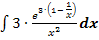

d.)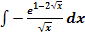

Lösung:

Zu 3a.)

Es soll das unbestimmte Integral 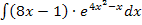berechnet werden. Das ist nicht schwer, denn man erkennt sofort, dass die Ableitung des Exponenten schon da steht. Der Exponent ist 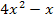;dies ergibt abgeleitet .

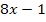Der erste Faktor des Produkts 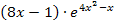ist also genau die Ableitung des Exponenten. Die Regel 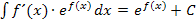lässt sich direkt anwenden. Damit erhalten wir schon die Lösung:

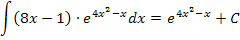
Zu 3b.)

Hier noch einmal die Angabe: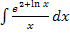

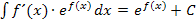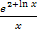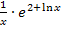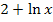Es ist nicht so leicht zu erkennen, dass sich dieses Integral ebenfalls mit Hilfe der Regel lösen lässt. Eigentlich ist der Trick, den wir anwenden müssen, ganz leicht;nur darauf zu kommen, ist nicht so einfach:Wir schreiben den Bruch als Produkt. An Stelle von kann auch schreiben. Nun ist leicht zu erkennen, dass genau die Ableitung des Exponenten ist.

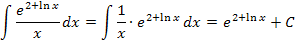
Zu 3c.)

Hier noch einmal das Integral, das zu berechnen ist: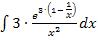

Wir verfahren im Prinzip, wie schon in Teilaufgabe 3b. und formen den Bruch so um, dass ein Produkt entsteht. Außerdem multiplizieren wir die Klammer im Exponenten aus.

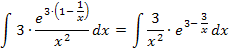
Nun betrachten wir den Exponenten 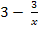. Wir leiten die Funktion 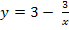in einer Nebenrechnung ab. Dazu könnte man die Quotientenregel anwenden, doch ist das gar nicht nötig. Schneller geht es, wenn man den Bruch mit Hilfe des Potenzgesetzes 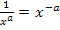umformt und dann mit der Regel 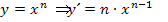ableitet. Anders gesagt:Man zieht den Exponenten beim Ableiten nach vorne und macht außerdem den Exponenten um 1 kleiner. (Das bedeutet, dass man den Exponenten nehmen und in Gedanken auf dem Zahlenstrahl um 1 nach links gehen muss.

---