1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Um F(x) abzuleiten, braucht man die Kettenregel;es handelt sich bei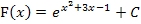 
schließlich um eine verkettete Funktion. Die innere Funktion ist 
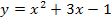;die äußere Funktion ist die e-Funktion 
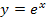. Laut Kettenregel muss zuerst die äußere Funktion abgeleitet werden. Die Ableitung von 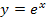ist bekanntlich 
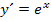. Die innere Funktion wird statt x hingeschrieben und dann nachdifferenziert, d.h. es wird nachher mit der Ableitung der inneren Funktion multipliziert. Die Ableitung der inneren Funktion 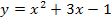ist 
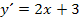. Es muss hier also mit 
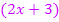nachdifferenziert werden. Die additive Konstante C fällt beim Ableiten natürlich weg. Daher gilt:
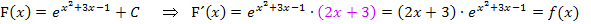
Da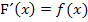 
gilt, haben wir gezeigt, dass die oben gezeigte Integration korrekt ist.
Bei jeder Funktion der Form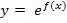 
muss beim Ableiten die Kettenregel angewendet werden. Es muss daher mit 
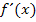nachdifferenziert werden. Allgemein gilt:
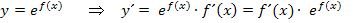
Soll man umgekehrt eine Funktion der Form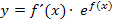 
integrieren, muss wieder diejenige Funktion herauskommen, die man ursprünglich abgeleitet hat, also 
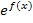. Daher muss zwangsläufig gelten:
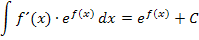
So kommt man auf diese Integrationsregel.
Wenn dir das noch nicht so ganz klar ist, solltest du ein paar Funktionen der Form 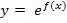zuerst ableiten und danach das Ergebnis wieder integrieren, beispielsweise die Funktionen 
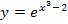und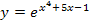 
. Machen wir das doch gemeinsam.
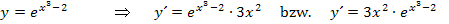
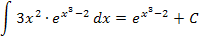
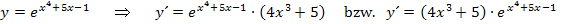
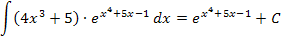
Hoffentlich leuchtet es dir nun ein, woher die Regel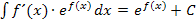 
kommt.
Hinweis:Die Integrationsregel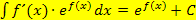 
kann auch bei Integralen von Produkten verwendet werden, deren erster Faktor nicht exakt der Ableitung des Exponenten entspricht, sondern nur einem Vielfachen davon. Dann benötigt man jedoch einen Ausgleichsfaktor, d.h. eine Zahl, die man vor das Integral schreibt, damit letztendlich doch der eine Faktor des Produkts mit der Ableitung des Exponenten übereinstimmt.
Aber Vorsicht:
Aus einem Integral darf man ausschließlich Konstanten, also Zahlen ohne x, herausziehen. Keinesfalls dürfen Ausdrücke, die x enthalten, aus einem Integral herausgezogen werden.
Daher kann die Regel 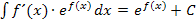wirklich nur dann angewendet werden, wenn ein Faktor des zu integrierenden Produkts zumindest ein Vielfaches der Ableitung des Exponenten ist. Der eine Faktor des Produkts, das man integrieren soll, muss also von den x-Potenzen her mit der Ableitung des Exponenten übereinstimmen. Du leitest also in Gedanken immer zuerst den Exponenten ab und schaust, ob diese Ableitung oder zumindest ein Vielfaches davon bereits da steht. Ist dies nicht der Fall, lässt sich die Integrationsregel 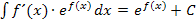nicht anwenden.
