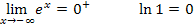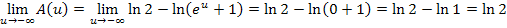Uneigentliche Integrale
(Statt der Zahl -3 kannst du natürlich auch irgendeine andere negative Zahl für u nehmen.)
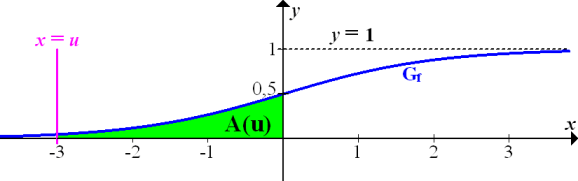
Abb.:Der Graph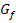 
der Funktion 
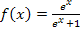und die Gerade x = u schließen mit den Koordinatenachsen das Flächenstück A(u) ein. Für u wurde hier als Beispiel die Zahl -3 gewählt.
Berechnung von A(u):
Nun berechnen wir die gesuchte Fläche A in Abhängigkeit von u, d.h. wir setzen ab sofort für u nichts Konkretes mehr ein, sondern rechnen mit u einfach so, als wäre u eine konkrete Zahl. Wegen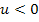 
stellt u eine negative Zahl dar. Deshalb integrieren wir von u bis 0 und nicht andersherum. Wir integrieren schließlich immer von links nach rechts. Nur unter dieser Voraussetzung und wenn der Funktionsgraph oberhalb der x-Achse verläuft – was hier der Fall ist – ergibt das Integral nämlich einen positiven Wert und entspricht der Fläche zwischen Graph und x-Achse. Die untere Grenze ist also u und die obere Grenze 0. Die obere Grenze ist 0, weil die gesuchte Fläche auf der rechten Seite von der y-Achse begrenzt wird. (Die Gleichung der y-Achse ist bekanntlich x = 0.) Das Integral 
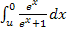entspricht somit genau der Fläche zwischen dem Graph von 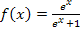und der x-Achse von x = u bis x = 0. Dieses Integral ist also die gesuchte Fläche A(u).
Berechnung des Integrals in Abhängigkeit von u:
Zuerst benötigen wir eine Stammfunktion zu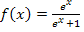 
. Da der Zähler des Bruchs genau die Ableitung des Nenners ist, kann die Integrationsregel 
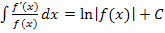verwendet werden.
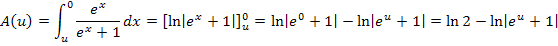
Die Betragsstriche sind unnötig, da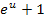 
immer positiv ist, egal was man für u einsetzt. Warum? Ganz einfach:Weil 
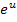immer positiv ist, muss 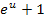erst recht positiv sein. Wir können die Betragsstriche somit weglassen. (Vorsicht:Würde von 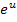etwas abgezogen werden, wäre das Ergebnis nicht immer positiv. So ist zum Beispiel 
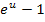nicht immer größer Null. Bei 
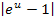dürfte man beispielsweise den Betrag nicht weglassen.)
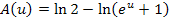
Eigentlich handelt es sich bei 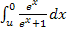um ein bestimmtes Integral, da keine der beiden Grenzen Unendlich oder eine Definitionslücke ist und auch keine Definitionslücke im Integrationsbereich liegt. Da wir aber bei A(u) noch u gegen 
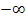gehen lassen sollen, bedeutet 
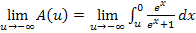eigentlich nichts anderes wie 
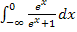und das ist letztendlich doch ein uneigentliches Integral. Ob man nun zuerst 
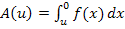bildet und dann 
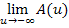berechnet oder gleich direkt 
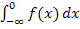bildet, läuft auf das Gleiche hinaus. Auf diese Art und Weise versteckt kommen uneigentliche Integrale des Öfteren in Abituraufgaben vor.
Nun berechnen wir den gesuchten Grenzwert.
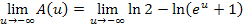
Zur Erinnerung: 
