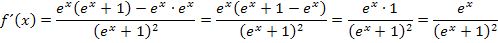Uneigentliche Integrale

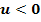d.) Berechne in Abhängigkeit von u die Fläche A(u) im II. Quadranten, die von , den Koordinatenachsen und der Gerade x = u mit begrenzt wird.

Berechne anschließend 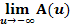und interpretiere das Ergebnis geometrisch anschaulich!

Lösung:

Zu 2a.)

Gegeben: 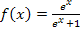mit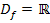

Es soll das Verhalten von 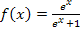im Unendlichen untersucht und die Gleichungen aller Asymptoten angegeben werden. Das bedeutet, dass man die Grenzwerte 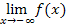und 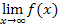berechnen soll. Definitionslücken hat die Funktion nicht;es gilt ja 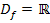. Daher existieren keine senkrechten Asymptoten. (Eine senkrechte Asymptote fällt schließlich immer mit einer Definitionslücke zusammen.) Es kann nur waagrechte oder schräge Asymptoten geben.

Zur Erinnerung:

Tipp:Leichter merken kann man sich diese beiden Grenzwerte in folgender etwas unmathematischen Schreibweise:

Der Grenzwert 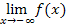lässt sich problemlos berechnen:Einfach bei 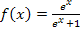für x in Gedanken 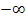einsetzen und dann statt 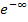die Zahl 0 oder genauer 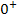schreiben und das Ergebnis ausrechnen.

Der Grenzwert 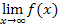macht etwas mehr Probleme, weil sich dabei der unbestimmte Ausdruck ergibt.

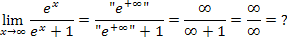
Leider kann man nicht allgemein sagen, was das ergibt. Wir wenden daher einen kleinen Trick an:Wir klammern im Zähler und im Nenner jeweils die höchste Potenz aus, das ist in diesem Fall natürlich 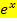. Nach dem Kürzen von 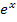lässt sich der Grenzwert ermitteln.

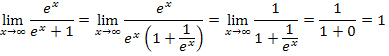
Dir ist nicht klar, warum 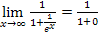gilt?

Ok, dann noch einmal, aber ganz langsam:Du setzt in Gedanken bei 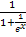für x erst einmal Unendlich ein.

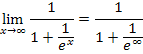
Du weißt außerdem, dass 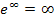ist. So ergibt sich folgendes:

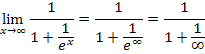
Jetzt ist vor allem die Frage zu beantworten, was ergibt. 1 durch eine riesig große Zahl geteilt, wird ganz ganz klein, also fast Null. Eine riesige Zahl passt schließlich fast gar nicht, praktisch Null mal, in die Zahl 1 hinein. Daher gilt: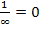

Insgesamt erhalten wir:

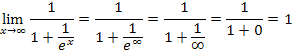
Anmerkung:Die soeben verwendete Schreibweise ist etwas unmathematisch. Sie wurde nur verwendet, damit du jeden Gedankenschritt besser nachvollziehen kannst. Eigentlich solltest du dir das alles nur im Kopf überlegen, aber so nicht hinschreiben. Am besten du schreibst das Ganze in Prüfungen folgendermaßen hin:

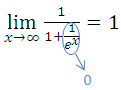
An dieser Schreibweise dürfte kein Lehrer etwas auszusetzen haben.

Zu 2b.)

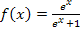
Um die Extrema zu ermitteln und das Monotonieverhalten von 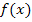zu untersuchen, brauchen wir natürlich die erste Ableitung. Wir bilden sie mit Hilfe der Quotientenregel.

---