Uneigentliche Integrale

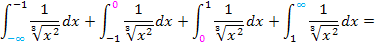
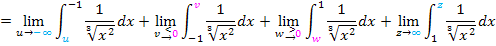
Puh, das wäre richtig viel Arbeit, dies alles auszurechnen! Das ersparen wir uns lieber, denn es geht erfreulicherweise auch schneller.

Um den Rechenaufwand zu verringern, nutzen wir hier die Tatsache, dass die Funktion 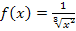achsensymmetrisch zur y-Achse ist. Zu erkennen ist dies an der geraden Potenz des Radikanden. Egal, ob man x oder – x in 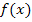einsetzt, es ergibt sich immer das Gleiche:

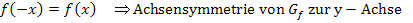
Nachweis der Achsensymmetrie:

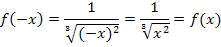
Für achsensymmetrische Funktionen gilt bekanntlich:

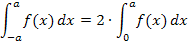
Auf unsere Aufgabe bezogen, bedeutet das:

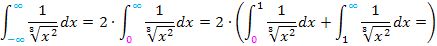
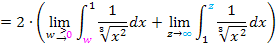
Es folgt die Umformung des Integranden mit Hilfe des Potenzgesetzes .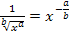

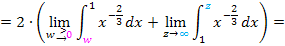
Nun ist die Integration mittels der Formel 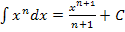möglich.

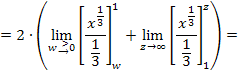
Wie du weißt, dividiert man durch einen Bruch, indem man mit dem Kehrwert multipliziert. Statt „durch ein Drittel“ rechnen wir daher „mal Drei“. Dann sieht die Stammfunktion deutlich besser aus.

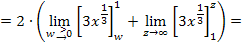
Mit dem Potenzgesetz 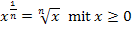ergibt sich:

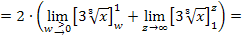
Nun setzen wir jeweils die Grenzen ein.

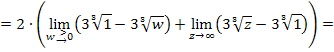
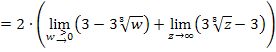
Jetzt müssen nur noch die beiden Grenzwerte berechnet werden und wir sind fertig.

Somit ergibt sich insgesamt:

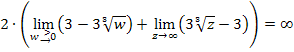
Daher gilt:

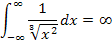
Das uneigentliche Integral hat keinen endlichen Wert. Man sagt, dass es divergiert.

Wenn im Gegensatz dazu ein uneigentliches Integral einen endlichen Wert annimmt, sagt man, dass es konvergiert.

In anderen Worten:Kommt bei einem uneigentlichen Integral eine konkrete Zahl heraus, dann konvergiert das Integral gegen diese Zahl. Ergibt sich bei einem uneigentlichen Integral dagegen Unendlich oder Minus-Unendlich, dann divergiert es.

Im Bsp. 1a.) haben wir gezeigt, dass gilt: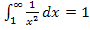

Dieses Integral konvergiert also gegen 1. Man kann auch einfach sagen, es ist konvergent.

Im Bsp. 1b.) haben wir gezeigt, dass gilt: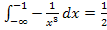

Dieses Integral ist ebenfalls konvergent;es konvergiert gegen den Wert .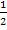

Im Bsp. 1c.) haben wir 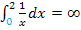berechnet. Dieses Integral divergiert. Man kann auch sagen, es ist divergent.

In einigen Abituraufgaben (G8) sind Aufgaben enthalten, die im Prinzip uneigentliche Integrale enthalten. Allerdings wird das uneigentliche Integral in der Regel nicht direkt als solches gefragt, sondern meist sind die Aufgaben so ähnlich formuliert wie im folgenden Beispiel die Teilaufgabe 2d.

2. Bsp.:Gegeben ist die Funktion 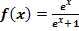mit .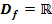

a.) Untersuche das Verhalten für 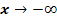und 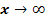. Gib die Gleichungen aller Asymptoten vo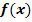n an!

b.) Untersuche das Monotonieverhalten der Funktion !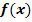

c.) Skizziere den Graph 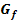mit Hilfe der bisherigen Ergebnisse!

---