Uneigentliche Integrale
Einen der beiden Ausdrücke müssen wir also entsprechend umformen. Wir entscheiden uns hier dafür,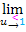 
in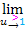 
umzuformen. Das geht folgendermaßen:
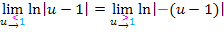
Auf Grund des Betrages ist das Minus-Zeichen letztendlich unnötig;wir können es wieder weglassen.
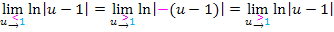
In diesem Fall erhält man daher für u gegen 1 bei linksseitiger Annäherung das gleiche Ergebnis wie bei der Annäherung von rechts.
Wir können daher folgende Rechnung durchführen:
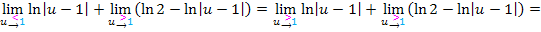
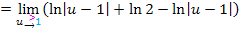
Jetzt kann zu einem einzigen Logarithmus zusammengefasst werden.
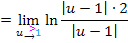
Dabei verwendete Logarithmus-Rechengesetze: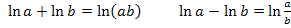 
Nun lässt sich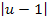 
kürzen. Dadurch ergibt sich:
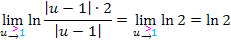
Durch das Kürzen ist u komplett herausgefallen. Du kannst bei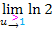 
den limes einfach vergessen;Es ergibt sich einfach der Wert ln2. Denn bei ln2 kannst du für u schließlich gar nichts einsetzen;es kommt ja gar kein u mehr vor. (Deshalb brauchst du jetzt u auch gar nicht mehr gegen 1 streben lassen.)
Zusammenfassung der Rechnung:
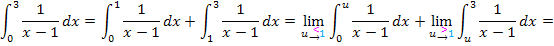
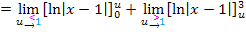
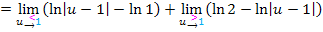
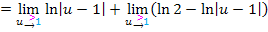
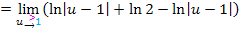
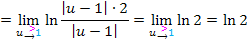
Zu 1e.)
Es soll das Integral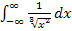 
berechnet werden. Dabei treten gleich zwei Probleme auf. Erstens sind beide Integrationsgrenzen „Problemstellen“ und zweitens liegt die Definitionslücke x = 0 im Integrationsbereich. Da man u nicht gleichzeitig gegen 
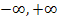und gegen 0 gehen lassen kann, müssen wir das Integral so in mehrere Teilintegrale zerlegen, dass jeweils nur eine Grenze eine „Problemstelle“ ist. An der Definitionslücke x = 0 müssen wir das Integral auf jeden Fall teilen. Außerdem muss zusätzlich einmal links von 0 und einmal rechts von 0 ein zusätzlicher Schnitt gesetzt werden. Dafür gibt es viele Möglichkeiten. Da wir allerdings möglichst einfache Zahlen als Grenzen wollen, entscheiden wir uns dafür bei -1, 0 und +1 „aufzuschneiden“.
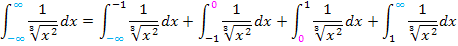
Die erste Schnittstelle bei x = -1 und die dritte bei x = +1 sind frei gewählt worden. Die Schnittstelle bei x = 0 ist durch die Definitionslücke vorgegeben. Bei x = 0 muss das Integral also zwangsläufig aufgeteilt werden. Anstatt bei x = -1 und bei x = +1 hättest du aber natürlich auch an zwei anderen Stellen schneiden können. Hauptsache du nimmst eine Zahl links von der Definitionslücke als erste Teilungsstelle, exakt die Definitionslücke als zweite und eine Zahl rechts von der Definitionslücke als dritte. Die erste und dritte Schnittstelle sind voneinander völlig unabhängig:Ihr Wert muss nicht zwangsläufig vom Betrag her gleich sein. So könntest du beispielsweise auch bei -3, 0 und +5 schneiden. Wir bleiben aber bei den Schnittstellen x = -1, x = 0 und x = +1. Mit diesen Zahlen rechnet es sich nachher am besten.
