Uneigentliche Integrale
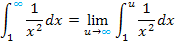
Nun berechnen wir das Integral;wir denken uns dabei u vorerst als „normale Zahl“. Wir rechnen also genauso, wie bei einem normalen bestimmten Integral:Stammfunktion F zu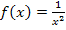 
ermitteln und in eckige Klammern (Grenzen an die rechte Klammer jeweils oben bzw. unten)schreiben. Davor steht natürlich immer 
.
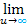Um 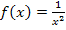besser integrieren zu können, formen wir mit dem Potenzgesetz 
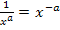um, dann lässt sich die Integrationsregel 
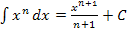anwenden.
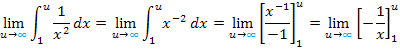
Dann werden die Grenzen eingesetzt, obere minus untere. Dadurch ergibt sich ein Term mit der Variablen u.
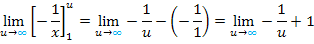
Zuletzt berechnen wir dann den Grenzwert 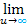des erhaltenen Terms. Für sehr große Werte von u wird 
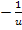sehr, sehr klein;also 
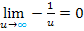. Damit ergibt sich:
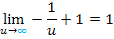
Die Fläche zwischen dem Graphen der Funktion 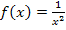, der senkrechten Gerade x = 1 und der x-Achse, die sich im I. Quadranten ins Unendliche erstreckt, ist somit nicht unendlich groß, sondern nähert sich an den Wert 1 an. Man kann sich das so vorstellen, dass die Fläche zwar immer noch ein klein wenig größer wird, je größer man die obere Grenze u macht, dass aber immer weniger dazu kommt. Der Flächeninhalt nimmt daher einen endlichen Wert an, -nämlich den Wert 1.
Zu 1b.)
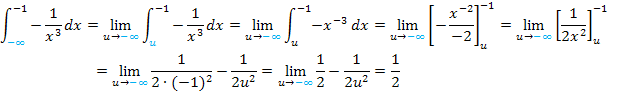
Zu 1c.)
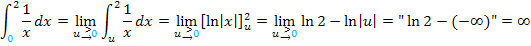
Erläuterungen zum Rechenweg:
Die Funktion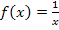 
hat an der Stelle x = 0 eine Definitionslücke;es gilt schließlich: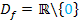 
Die untere Grenze des Integrals fällt also mit der Definitionslücke zusammen. Um das Integral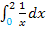 
zu berechnen, ersetzen wir daher die Zahl 0 durch den Buchstaben u und schreiben vor das Integral 
. Das Größer-Zeichen bedeutet, dass wir uns von rechts an die Zahl 0 annähern. Das ist wichtig, denn für die Berechnung des Grenzwertes ist es nachher entscheidend, ob man sich von links oder von rechts an die Null annähert. Dass man den rechtsseitigen Grenzwert bilden muss, ergibt sich aus den vorgegeben Grenzen:Es soll schließlich das Integral von 0 bis 2 berechnet werden. Die obere Grenze 2 ist logischerweise größer als 0. Wir befinden uns also in einem Intervall, das rechts von 0 liegt. (Hätte im Gegensatz dazu beispielsweise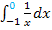 
berechnet werden sollen, hätte der linksseitige Grenzwert 
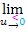berechnet werden müssen, weil man sich dann in einem Intervall links von 0 befunden hätte.)
Nun zur Berechnung des Integrals. Die Umformung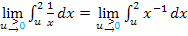 
bringt uns nicht weiter, denn die Integrationsregel 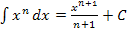lässt sich hier nicht anwenden. Diese Formel gilt nicht für 
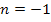, da der Nenner Null ergeben würde. Du würdest 
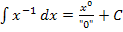erhalten;das stimmt natürlich nicht!
Stattdessen musst du die Formel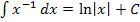 
verwenden.
