Uneigentliche Integrale

Hat das Integral als obere Grenze 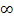und als untere Grenze die Zahl a, wobei gilt a 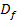, schreibt man:

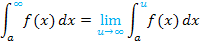
Hat das Integral als untere Grenze 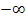und als obere Grenze die Zahl a, wobei gilt a 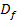, schreibt man:

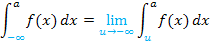
Hat das Integral die Definitionslücke b als obere Grenze und die Zahl a als untere Grenze mit a 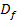, schreibt man:

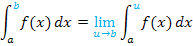
Dabei muss die Annäherung an die Definitionslücke b von der jeweils korrekten Seite vorgenommen werden. Entweder muss der rechtsseitige oder der linksseitige Grenzwert gebildet werden. Das hängt davon ab, ob die untere Grenze a kleiner ist als b oder umgekehrt b kleiner ist als a. Wenn gilt a <b, muss der linksseitige Grenzwert berechnet werden, weil die zum Integral gehörige Fläche links von der Definitionslücke b liegt.

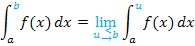
Hat das Integral die Definitionslücke b als untere Grenze und die Zahl a als obere Grenze mit a 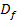, schreibt man:

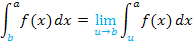
Auch dabei muss die Annäherung an die Definitionslücke b wieder von der jeweils korrekten Seite vorgenommen werden. Entweder muss der rechtsseitige oder der linksseitige Grenzwert gebildet werden. Das hängt wieder davon ab, ob die untere Grenze b kleiner ist als a oder umgekehrt a kleiner ist als b. Wenn gilt b <a, muss der rechtsseitige Grenzwert berechnet werden, weil die zum Integral gehörige Fläche rechts von der Definitionslücke b liegt.

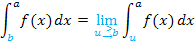
Sind beide Integrationsgrenzen „Problemstellen“, muss das Integral an einer beliebigen Stelle c 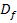aufgeteilt werden.

Hat das Integral als untere Grenze 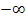, als obere Grenze 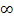und keine Definitionslücken, schreibt man:

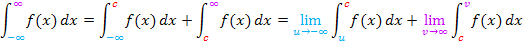
Die Schnittstelle c kann dabei frei gewählt werden. Am besten nimmt man eine Zahl, mit der sich gut rechnen lässt, wie zum Beispiel c = 0 oder c = 1.

Liegt im Integrationsbereich eine Definitionslücke, muss das Integral an genau dieser Stelle geteilt werden. Genauer erklärt wird das an Hand der Berechnungen von 1d.) und 1e.). Siehe unten!

Am besten verstehst du das sicher an konkreten Beispielen. Deshalb gleich die Berechnungen der oben aufgeführten Beispiele.

Zu 1a.)

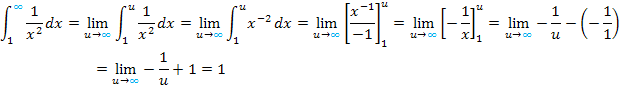
Erläuterungen zum Rechenweg:

Das Integral 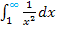hat als obere Grenze 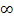. Die Funktion 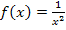hat bei x = 0 eine Definitionslücke;sie liegt aber nicht im Integrationsbereich, also nicht zwischen der unteren Grenze 1 und der oberen Grenze 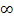. Die Definitionslücke macht uns daher keine Probleme, nur die obere Grenze 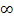ist die Schwierigkeit. Wir verwenden anstatt der oberen Grenze 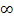den Buchstaben u und schreiben 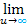vor das Integral.

---