Uneigentliche Integrale

Anschaulich bedeutet das, dass die Fläche zwischen dem Funktionsgraphen und den Koordinatenachsen, die sich im II. Quadranten ins Unendliche erstreckt, nicht unendlich großist, sondern gegen den Wer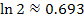t geht.

In der folgenden Abbildung ist die berechnete Fläche zu sehen.

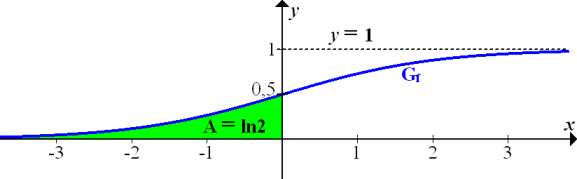
Zusätzliche Aufgabe:

Zur Übung könntest du außerdem rechnerisch überprüfen, ob auch die Fläche zwischen dem Graphen von 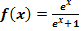, den Koordinatenachsen und der waagrechten Asymptote y = 1 für 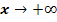einen endlichen Wert annimmt.

Lösung der Zusatzaufgabe:

Die Fläche zwischen zwei Funktionen berechnet man bekanntlich, indem man die untere Funktion von der oberen abzieht und davon das Integral bildet. In diesem Fall liegt y = 1 oberhalb von 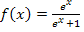. Es muss daher das folgende Integral berechnet werden:

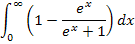
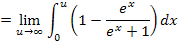
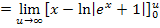
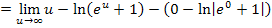
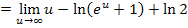
Um den Grenzwert zu berechnen, muss alles zu einem Logarithmus zusammengefasst werden. Statt u schreiben wir daher .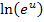

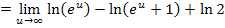
Die Anwendung der Logarithmusrechengesetze 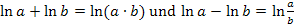ergibt:

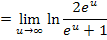
Wir klammern im Nenner 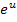aus, damit wir nachher 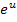kürzen können. Dadurch lässt sich nachher der Grenzwert berechnen.

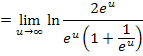
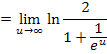
Mit 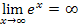ergibt sich 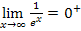und somit folgt:

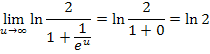
Die Fläche zwischen dem Graphen von 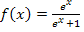, den Koordinatenachsen und der waagrechten Asymptote y = 1, die sich im I. Quadranten ins Unendliche erstreckt, nimmt also einen endlichen Wert an;sie geht gegen ln2. Diese Fläche ist also genauso großwie die Fläche zwischen 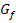und den Koordinatenachsen, die sich im II. Quadranten ins Unendliche erstreckt. Das ist auf die Punktsymmetrie des Graphen 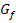zum Punkt 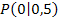zurückzuführen. (Vergleiche Abbildung oben.)

---