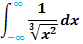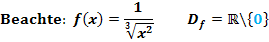Uneigentliche Integrale
Unter einem uneigentlichen Integral versteht man Integrale, die als untere oder auch als obere Grenze entweder eine Definitionslücke oder 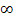 bzw.
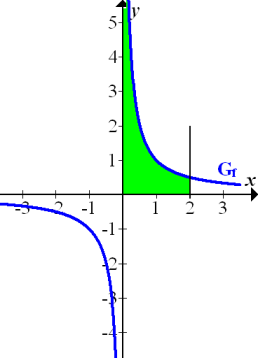
bzw. 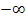 haben. Manchmal sind zwar beide Grenzen konkrete Zahlen, die in der Definitionsmenge enthalten sind, aber es liegt eine Definitionslücke innerhalb des Integrationsbereichs;auch solche Integrale werden als uneigentliche Integrale bezeichnet. Es handelt sich bei uneigentlichen Integralen praktisch um Flächen, die sich teilweise ins Unendliche erstrecken. (Genau genommen um die Flächenbilanz. Siehe auch:Das bestimmte und das unbestimmte Integral.) Nun wirst du wahrscheinlich glauben, dass solche Flächen unendlich großsind;aber genau das ist nicht immer der Fall! Die Fläche zwischen dem Graph einer Funktion
haben. Manchmal sind zwar beide Grenzen konkrete Zahlen, die in der Definitionsmenge enthalten sind, aber es liegt eine Definitionslücke innerhalb des Integrationsbereichs;auch solche Integrale werden als uneigentliche Integrale bezeichnet. Es handelt sich bei uneigentlichen Integralen praktisch um Flächen, die sich teilweise ins Unendliche erstrecken. (Genau genommen um die Flächenbilanz. Siehe auch:Das bestimmte und das unbestimmte Integral.) Nun wirst du wahrscheinlich glauben, dass solche Flächen unendlich großsind;aber genau das ist nicht immer der Fall! Die Fläche zwischen dem Graph einer Funktion 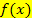 und seiner Asymptote kann einen endlichen Wert haben, also einen konkreten Zahlenwert, obwohl sich die Fläche ins Unendliche erstreckt.
und seiner Asymptote kann einen endlichen Wert haben, also einen konkreten Zahlenwert, obwohl sich die Fläche ins Unendliche erstreckt.
Beispiele für die unterschiedlichen Fälle uneigentlicher Integrale:
|
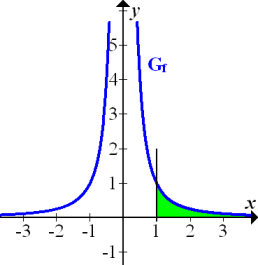
1a.) Integral mit der oberen Grenze
|
|
|
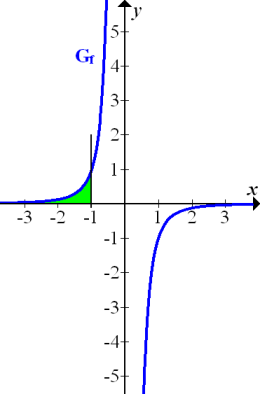
1b.) Integral mit der unteren Grenze
|
|
|
1c.) Integral mit Definitionslücke als Grenze
|
|
|
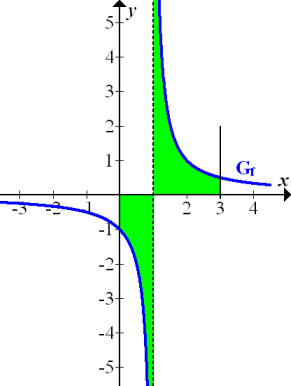
1d.) Integral einer Funktion mit Definitionslücke im Integrationsbereich
Die Definitionslücke x = 1 liegt im Integrationsbereich, also zwischen der unteren Grenze 0 und der oberen Grenze 3!
|
|
|
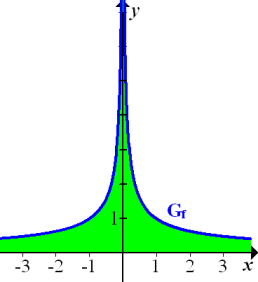
1e.) Integral von
|
|
Wie berechnet man nun solche Integrale? Im Prinzip ist das gar nicht so schwer. Statt 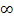 bzw.
bzw. 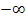 oder der Definitionslücke schreibt man erst einmal zum Beispiel u und berechnet dann den entsprechenden Grenzwert.
oder der Definitionslücke schreibt man erst einmal zum Beispiel u und berechnet dann den entsprechenden Grenzwert.

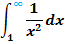
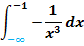
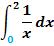
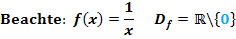
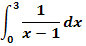
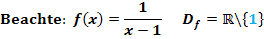
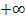 mit Definitionslücke im Integrationsbereich
mit Definitionslücke im Integrationsbereich