Die Integralfunktion und der HDI
Der Nenner der Ableitung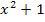 
ist immer positiv, da zu einer geraden Potenz (kann nicht negativ sein) noch etwas dazu gezählt wird. Der Zähler der Ableitung besteht nur aus der negativen Zahl -1 und ist deshalb immer negativ. Wegen Minus durch Plus ist Minus ist die Ableitung 
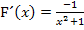immer negativ;die Funktion F ist somit streng monoton fallend.
Zu 4b.)
Es handelt sich bei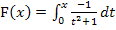 
um eine Integralfunktion;es steht ja die Variable x oben am Integral. Jede Integralfunktion hat mindestens eine Nullstelle, nämlich bei ihrer unteren Grenze. In diesem Fall ist die untere Grenze 0. Daher hat F bei 
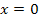eine Nullstelle.
Nun muss aber noch gezeigt werden, dass es sich um die einzige Nullstelle handelt. Da du das Integral nicht ausrechnen kannst, lässt sich keine integralfreie Darstellung von F finden. Daher können wir nicht einfach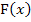 
in integralfreier Form gleich Null setzen und zeigen, dass dabei wirklich keine andere Lösung als 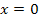herauskommt. Wir müssen uns etwas anderes einfallen lassen. Bloßwas?
Kleiner Tipp:Verwende das Ergebnis von Teilaufgabe 4a.)!
In Teilaufgabe 4a.) haben wir bereits gezeigt, dass F streng monoton fallend ist. Eine stetige Funktion, die streng monoton ist, kann die x-Achse nur einmal schneiden. (Damit es eine weitere Nullstelle geben könnte, müsste sich das Monotonieverhalten der Funktion ändern.) Stelle dir das doch mal anschaulich vor:Eine stetige Funktion hat keine Sprungstellen, verläuft also in einem Stück. (Du kannst dem Graph einer stetigen Funktion mit der Fingerspitze folgen ohne loszulassen. Siehe auch:Stetigkeit) Wenn eine Funktion immer fällt, schneidet sie die x-Achse maximal einmal. (Dasselbe gilt natürlich auch für streng monoton steigende Funktionen.) Betrachte dazu die folgende Skizze!
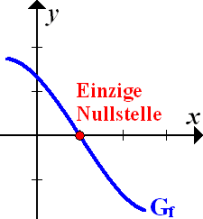
Abb.:Graph 
irgendeiner streng monoton fallenden Funktion, er kann die x-Achse höchstens einmal schneiden, also höchstens eine Nullstelle haben.
Damit der Graph einer stetigen Funktion die x-Achse ein zweites Mal schneiden könnte, müsste er teils fallen und teils steigen, also seine Monotonie ändern. Es müsste einen Extrempunkt geben.
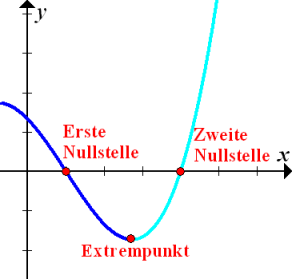
Abb.:Graph irgendeiner nicht monoton verlaufenden, aber stetigen Funktion:In Dunkelblau der fallende Teil des Graphen, in Hellblau der steigende Teil. Er kann die x-Achse auch öfter als einmal schneiden;so eine Funktion kann somit mehr als eine Nullstelle haben.
