Die Integralfunktion und der HDI
4. Bsp.:Anwendung des HDI
Betrachtet wird die Integralfunktion:
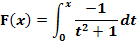
a.) Untersuche das Monotonieverhalten von F! Hat F Extrema? (Wenn ja, gib auch die Art und Lage der Extrempunkte von F an.)
b.) Zeige, dass die Funktion F genau eine Nullstelle besitzt. Wo liegt diese Nullstelle?
Die folgenden beiden Teilaufgaben sind nur für Schüler geeignet, die bereits die zweite Ableitung und das Thema „Wendepunkte“ im Unterricht behandelt haben.
c.) Beweise:Die Funktion F besitzt genau einen Wendepunkt. Gib auch die Koordinaten des Wendepunkts an.
d.) Stelle die Gleichung der Wendetangente auf.
Lösung:
Bei dieser Aufgabe keinesfalls versuchen, selbst zu integrieren! Die Integrandenfunktion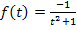 
ist ein Quotient;Zähler und Nenner dürfen nicht einzeln integriert werden. Würdest du bei 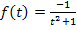den Zähler und Nenner doch einzeln integrieren, ergäbe sich 
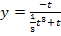. Die Funktion 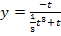ist aber keine Stammfunktion zu 
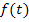. Wenn du 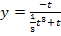mit Hilfe der Quotientenregel wieder ableitest, wirst du feststellen, dass sich nicht 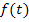ergibt. Somit ist klar, dass 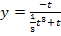keine Stammfunktion zu 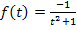sein kann. Du kannst bei dieser Aufgabe keine Stammfunktion finden. Eine Art „Quotientenregel zum Integrieren“ gibt es leider nicht. (Wie man manche Quotienten dennoch integrieren kann, wird im Teil Weitere Integrationsregeln besprochen.) Es ist dir nicht möglich eine integralfreie Darstellung der Funktion 
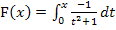ermitteln. Dennoch ist die Aufgabe für dich lösbar.
Du musst einfach den HDI, also den Zusammenhang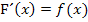 
verwenden.
Hier noch einmal die gegebene Integralfunktion: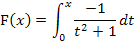 
Zu 4a.)
Um die Monotonie (d.h. das Steigungsverhalten) von F herauszufinden, brauchen wir die erste Ableitung von F.
Laut HDI gilt: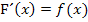
Man muss also einfach die Funktion nehmen, die direkt hinter dem Integralzeichen steht und t durch x ersetzen. Schon hat man F´(x) ermittelt.
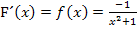
Normalerweise würdest du nun F´(x) gleich Null setzen, um eventuell vorhandene Extrema zu berechnen. (Bei einem Extremum verläuft die Tangente waagrechte, so dass die Steigung bzw. erste Ableitung an dieser Stelle gleich Null sein muss.) Das Nullsetzen der Ableitung ist hier jedoch gar nicht nötig. Man erkennt sofort, dass die Ableitung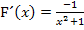 
gar nicht gleich Null werden kann, denn der Bruch enthält im Zähler kein x. Ein Bruch kann schließlich nur dann gleich Null werden, wenn der Zähler gleich Null wird. Der Zähler ist hier jedoch immer ungleich Null, denn die Zahl -1 kann schließlich nicht Null werden. Die Ableitung von F kann daher nicht gleich Null werden;F hat keine Punkte mit waagrechten Tangenten und somit keine Extrema.
